Retângulos são figuras geométricas planas que possuem quatro lados, sendo a medida dos lados paralelos iguais. Eles também possuem quatro ângulos retos, ou seja, seus ângulos internos medem todos 90°.
Iremos, agora, discutir o valor da área do retângulo e sua fórmula. Confira essas e outras informações completas só aqui, no Gestão Educacional!
O que é área?

O cálculo da área de um local nos mostra a quantidade de espaço que aquela região contém. Para conseguirmos medir essa quantidade de espaço, utilizamos as unidades de área.
Nossas unidades de área podem ser centímetros quadrados, metros quadrados, etc.
Vamos pensar, nesse momento, no centímetro quadrado. Ele é uma unidade de área representada por um pequeno quadrado que possui 1cm de lado, como mostra a figura abaixo.
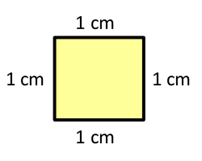
Podemos calcular a área de uma região retangular colocando vários desses quadradinhos dentro dela.
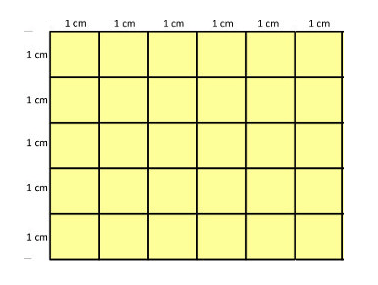
Contando um a um, percebemos que dentro desse retângulo temos 30 quadradinhos pequenos. Porém, podemos também perceber que, se cada quadradinho tem 1cm, o lado que possui 5 quadradinhos terá 5 centímetros, enquanto o outro que possui 6 quadradinhos terá 6 centímetros, como mostra a imagem abaixo.
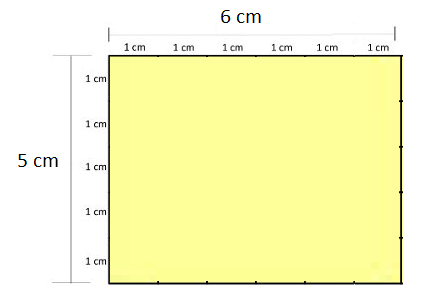
Podemos, então, calcular a área desse retângulo multiplicando 5 por 6.
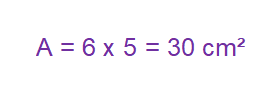
Fórmula do cálculo de área do retângulo
Para calcular essa área sem precisar contar quadrados, podemos multiplicar as medidas dos seus lados. Portanto, a área será dada por:
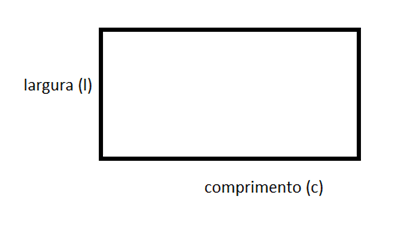
- A = c. l, sendo c o comprimento e l a largura.
Exemplos
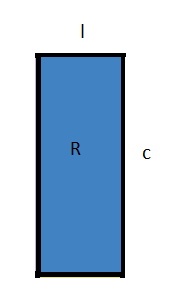
Considere uma região retangular R azul de comprimento (c) e largura (l), em que c e l são números reais.
Construindo uma região quadrada, cuja medida dos lados é c + l, a qual contém duas cópias de R e mais duas regiões quadradas, uma cujo lado mede c (quadrado lilás) e outra cujo lado mede l (quadrado amarelo).
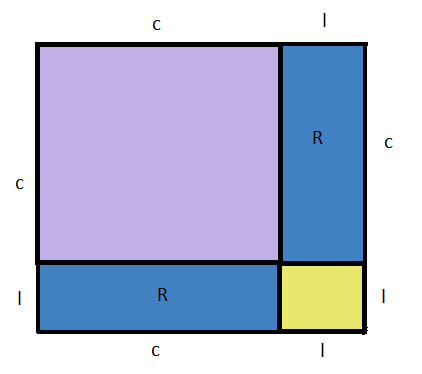
A medida dos lados dessa região quadrada, formada pelas figuras em amarelo, lilás e azul, é dada por (c+l). Portanto, a área dessa região quadrada Q é dada pelo quadrado de uma soma:
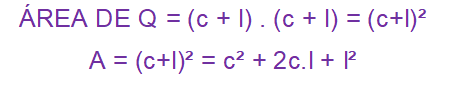
Como as regiões quadradas lilás e amarelo têm áreas iguais a l² e c², concluímos que: A = c² + l² + 2. (área de R).
Concluímos, então, que a área da região R em azul é igual a c.l
Exercícios Resolvidos
1) Determine a área da região retangular abaixo:
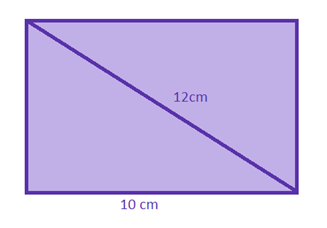
Pelo Teorema de Pitágoras, podemos fazer:
12² = 10² + x ²
144 = 100 + x²
X = 66 cm²
2) Uma caixa de creme dental tem forma de bloco retangular com as seguintes dimensões: 3cm, 4cm e 18cm. Determine a área da superfície.
Abrindo essa caixa, vamos ter algo parecido com o esquema:
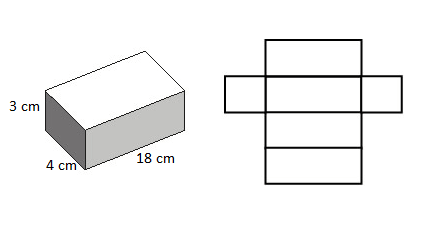
Temos, portanto, 2 retângulos de 10x4cm, dois retângulos de 4x18cm, e 2 retângulos de 3x4cm.
Calculando a soma das áreas, teremos:
(2x18x4) + (2x3x18) + (2x3x4) = 276 cm²





