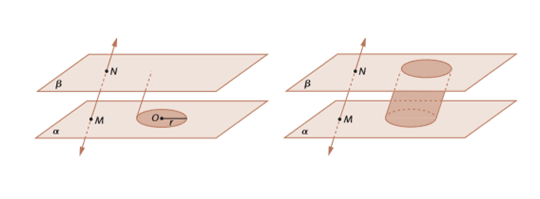
O cilindro, o cone e a esfera são considerados corpos redondos. Vamos imaginar dois planos distintos e paralelos entre si, ou seja, planos diferentes que não possuem pontos em comum ou se intersectam.
Um desses planos iremos denominar α e o outro iremos chamar de β. Imagine também uma reta MN, na qual o ponto M pertence ao plano α e o ponto M pertence ao plano β. Iremos também acrescentar uma circunferência contida no plano α de centro O e raio r.
Dessa forma, chamamos de cilindro circular a reunião de todos os seguimentos de reta que unem o círculo ao plano β, sendo esses segmentos paralelos e congruentes ao seguimento MN. Ou seja, esses seguimentos não formam ângulos entre si e são idênticos.
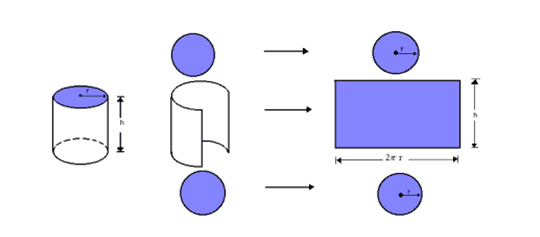
Planificação
A partir dessa definição de cilindro, podemos também, intuitivamente, imaginar que o cilindro reto é formado por duas bases e uma superfície lateral. Suas bases são circunferências e sua superfície lateral, ao ser planificada, é um retângulo.
Podemos definir a altura do cilindro como o tamanho do seguimento de reta que liga as duas bases.
Os dois maiores lados desse retângulo (que é a lateral do cilindro reto) têm a medida h, que é a altura do cilindro. Os outros dois lados restantes possuem a mesma medida que o comprimento da circunferência da base.
Chamamos a reta que passa pelo centro das duas bases do cilindro de eixo. Chamamos também de Geratriz todos os seguimentos que são paralelos ao eixo, e suas extremidades são os pontos que estão nas duas bases.

Categorias de Cilindros
Cilindros retos são aqueles em que a geratriz (altura) é perpendicular à sua base. Consequentemente, o eixo é perpendicular aos planos das bases.
Cilindros oblíquos são aqueles em que o eixo não é perpendicular à sua base.
Uma informação importante é que a altura e a geratriz de um cilindro possuem a mesma medida apenas se estivermos falando de um cilindro reto.
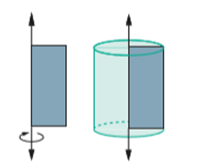
Imagine agora um retângulo. Essa região retangular tem um de seus lados colados em uma reta. Ao girarmos essa reta em torno do próprio eixo, como mostra a imagem, podemos obter um cilindro. Por isso, podemos também chamar o cilindro circular reto de cilindro de revolução, pois ele pode ser gerado pelo giro completo de uma seção retangular em torno do eixo.
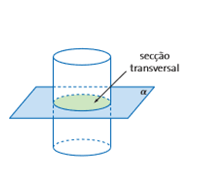
Secções de um cilindro
Classificamos como secção transversal o círculo que surge ao fazermos a intersecção do cilindro com um plano paralelo as suas bases. Basicamente, vamos “cortar” o cilindro horizontalmente e podemos então observar um círculo congruente às bases.
Já a secção meridiana de um cilindro segue a mesma ideia descrita acima, porém iremos “fatiar” o cilindro verticalmente, ou seja, iremos fazer a intersecção do cilindro com um plano que contém o seu eixo. O resultado disso é uma secção meridiana retangular no caso do cilindro reto.
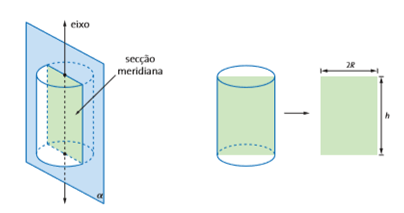
Caso a secção meridiana desse cilindro seja um quadrado, temos então o caso de um cilindro reto.
Área da superfície de um cilindro reto.
Relembrando a planificação desse cilindro, temos então um retângulo e duas circunferências.
Podemos calcular a área lateral (área do retângulo) multiplicando seus lados. Lembrando que um dos seus lados tem o mesmo tamanho que o comprimento de uma circunferência, temos:
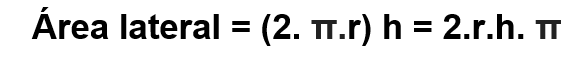
A área das bases é a área somada das duas circunferências. Área da Base = 2.Ab = 2.π.r²]
Fazendo a área total, temos:

Volume do cilindro
O volume do cilindro é calculado da mesma maneira que calculamos o volume de um prisma: V = Ab.h, sendo Ab é a área da base.
Exercícios Resolvidos
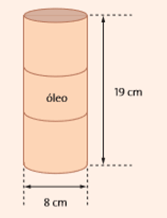
1. Quantos centímetros quadrados de material são usados, aproximadamente, para fabricar a lata de óleo indicada abaixo?
Resolução:
Diâmetro = 8 cm r = 4 cm h = 19 cm.
Vamos resolver esse problema em função de π.
Al = 2 πrh = 2 π . 4 . 19 = 152π
2Ab = 2. (πr²) = 2.4². π = 32 π
At = 152 π + 32 π = 184 π cm² de material.
- O reservatório de tinta de uma caneta esferográfica tem forma cilíndrica. Seu diâmetro é de 2mm e seu comprimento é de 12cm. Quantos ml de tinta podem ser acondicionados nesse reservatório?
Resolução:
Diâmetro: 2 mm = 0,2 cm. H = 12 cm.
V = Ab.h = (πr²).h = π.(0,1)².12 = 0,12π ml de tinta = 0,3768 ml aproximadamente.





