Denomina-se circunferência trigonométrica a circunferência orientada, de centro O na origem do sistema de coordenadas cartesianas ortogonais, cujo raio tem 1 unidade de comprimento e o sentido positivo é o anti-horário.
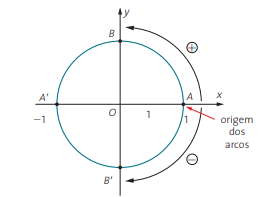
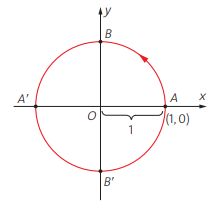
À circunferência trigonométrica de centro O vamos associar um sistema de coordenadas cartesianas ortogonais, fixando o ponto A de coordenadas (1, 0) como origem dos arcos, como mostra a figura abaixo:
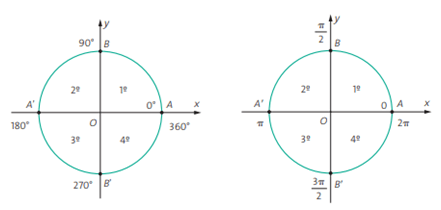
Os eixos x e y dividem a circunferência trigonométrica em quatro partes congruentes, chamadas quadrantes, numeradas de 1 a 4 e contadas a partir de A, no sentido positivo.
Podemos encontrar algumas observações:
- Os pontos A, B, A’ e B’ são pontos dos eixos e por isso não são considerados pontos dos quadrantes;
- Para todo ponto (x, y) pertencente à circunferência trigonométrica, temos -1 ≤ x ≤ 1 e –1 ≤ y ≤ 1. Ou seja, não existirá nenhum ponto pertencente à circunferência trigonométrica de coordenadas que não estejam nesses intervalos, como (2,-2).
Arcos e ângulos
Vamos definir alguns importantes conceitos para se entender o funcionamento da circunferência trigonométrica.
Arco geométrico é uma das partes da circunferência delimitada por dois pontos, incluindo-os. Se os dois pontos coincidirem, teremos arco nulo ou arco de uma volta.
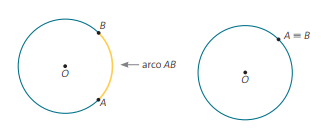
A medida e o comprimento de um arco são dados da seguinte maneira: considere um ponto A sobre uma circunferência de raio r e centro O. Deslocando-se o ponto A sobre a circunferência, ele percorre uma distância l ao mesmo tempo que gira um ângulo α em torno do centro O. Esse movimento do ponto A descreve um arco de circunferência de medida α e comprimento l.
Como você já pode ter estudado em física, toda grandeza deve possuir uma unidade de medida, por exemplo, a velocidade é medida em metros por segundo (m/s) e a força F é medida em Newtons (N). Com relação à circunferência trigonométrica, para definir a medida α de um arco, usam-se geralmente unidades como o “grau” e o “radiano”. Para o comprimento l usam-se, em geral, unidades como “metro”, “centímetro”, “quilômetro”, etc.
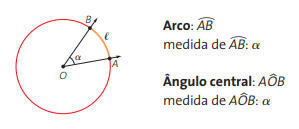
O arco é sempre relacionado ao seu ângulo central: todo arco de circunferência tem a mesma medida do ângulo central que o subtende. Por exemplo, o arco AB, abaixo, tem como medida o ângulo central AÔB de medida α.
O comprimento da circunferência é dado por:
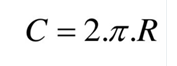
Unidades para medir arcos de circunferência (ou ângulos)
As unidades mais usadas para medir arcos de circunferência e seus ângulos correspondentes são o grau e radiano.
Podemos defini-los como:
- Grau: quando dividimos uma circunferência em 360 partes iguais, cada uma dessas partes é um arco de um grau (1°);
- Radiano: um arco de um radiano (1 rad) é um arco cujo comprimento é igual ao raio da circunferência. Ou seja, se temos um arco de medida 1 radiano, seu ângulo central irá também medir 1 radiano.
Por exemplo, se temos um ângulo central de medida 2 radianos, então ele é o ângulo de um arco de medida 2 radianos e comprimento de 2 raios. Se temos um ângulo central de medida α radianos, então ele subtende um arco de medida α radianos e comprimento de α raios.
Assim, se a medida α do arco for dada em radianos, teremos o comprimento l dado por: l = α.r.
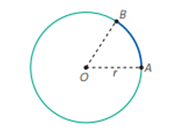
Esticando” o arco AB, a medida do segmento obtido será igual à do raio:
Existem outras unidades para medir arcos, por exemplo, o grado, que é um arco obtido a partir da divisão da circunferência em 400 partes iguais. Porém, as unidades mais usadas são o grau e o radiano.
Uma volta completa no círculo trigonométrico corresponde a 360°.
Relação entre arco e graus
Sabendo que um arco de 180° mede π rad, podemos fazer a conversão de unidades usando uma regra de três simples. Porém, recomendamos que você se acostume a fazer as principais conversões entre grau e radiano mentalmente, sem recorrer à regra de três. Esse procedimento é muito simples se observarmos que:
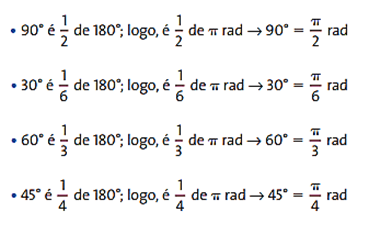
Arcos côngruos ou congruentes
Toda vez que o ponto da circunferência, final do arco iniciado em (1, 0), é o mesmo para dois arcos diferentes (por exemplo, 0 e 2π), chamamos esses arcos de arcos côngruos ou congruentes.
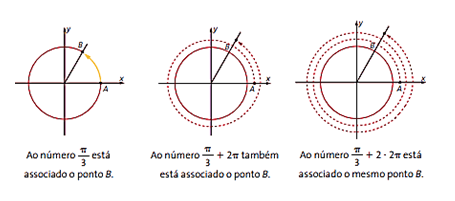
Observe que, no exemplo acima, os três arcos são delimitados pelos mesmos pontos A e B.
Na primeira figura, o ponto deslocou-se π/3 ou 60° de A até B. Na segunda figura, o ponto deslocou-se uma volta inteira (2π ou 360°) e mais π/3 ou 60°; ou seja, deslocou-se 7π/3 p ou 420°. Na terceira figura, o ponto deslocou-se duas voltas inteiras (2 . 2π ou 2 . 360°) e mais π/3 ou 60°; ou seja, 13π/3 p ou 780°.
Portanto, arcos côngruos diferem entre si 2π, que é o comprimento de cada volta. Para achar arcos côngruos basta somar ou subtrair 2π ou 360°, porém nunca subtraia até chegar a medidas negativas.
Exercício resolvido
1) Converta 30° em radianos.
Resolução:
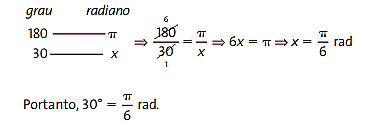
As propriedades da potenciação são ferramentas que simplificam operações envolvendo exponenciação. Conheça cada uma delas!
👉 Continue Lendo.. Clique aqui





