Expressões algébricas são usadas em equações e fórmulas que possuem incógnitas. Portanto, diferente das expressões numéricas, teremos agora, além de números e operações, letras que vão representar valores que não conhecemos. Chamamos o número desconhecido de incógnita.
Chamamos de álgebra essa parte da matemática na qual usamos fórmulas e calculamos expressões algébricas. A álgebra é uma ferramenta tanto para a matemática quanto para outras áreas do conhecimento.
Diferença entre expressão numérica e expressão algébrica
Em expressões numéricas, temos apenas operações com números. Veja o exemplo:
- 3 + 6 x 2 – 6 = 3 + 12 – 6 = 9
Já em expressões algébricas, temos letras que representam valores que não conhecemos. Veja o exemplo a seguir:
- X² – 3x + 5 = 0
Nas expressões algébricas, os números que estão sendo multiplicados pelas incógnitas (letras na equação) são chamados de coeficientes. Esses coeficientes multiplicam o valor atribuído à incógnita. Veja o exemplo:
- 3x² – 4x = 7. Nesse caso, 3 e 4 são coeficientes.
As propriedades que usávamos nas expressões numéricas podem ser usadas nas expressões algébricas.
Sabemos que a multiplicação é comutativa, ou seja, a ordem dos fatores não altera o produto. O mesmo vale nas expressões algébricas. Podemos, então, generalizar isso da seguinte forma:
- X . Y = Y . X
Nessas expressões, também são válidas as propriedades distributivas da multiplicação em relação à adição, técnica que chamamos popularmente de “chuveirinho”.
Veja o seguinte exemplo:
- 5 . (a + 7) = 5a + 35
Além disso, a ordem para resolver uma expressão algébrica segue a mesma das expressões numéricas.
Resolvemos primeiramente as potências e as raízes, depois a multiplicação ou divisão e por último adição e subtração, sempre na ordem que aparecem, que é da esquerda para a direita.
Para conhecer mais sobre expressões numéricas, veja o conteúdo completo delas, clicando aqui.
Exemplos de expressões algébricas
Como já foi dito, a álgebra é utilizada em diversas áreas. Na matemática, um interessante exemplo são os polinômios, expressões em que a variável x tem como expoente valores iguais ou maiores que 1.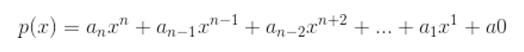
Para conhecer mais sobre polinômios, clique aqui e confira um conteúdo completo.
Na física, as fórmulas empregadas para descrever os fenômenos também são expressões algébricas. Para expressar a velocidade média de um corpo, usamos uma fórmula: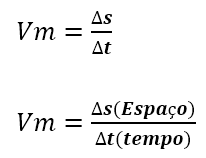
Se, por exemplo, soubermos a velocidade média de um móvel e a quantidade de tempo que ele utilizou para percorrer uma certa distância, podemos encontrar o espaço percorrido por ele.
Na química, também utilizamos expressões algébricas para montar fórmulas. O coeficiente de solubilidade é calculado pela seguinte fórmula: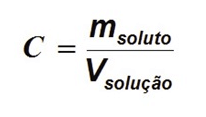
Usando letras para resolver problemas – equações
Nesse tipo de problema, usamos letras para representar números desconhecidos e depois traduzimos o enunciado do problema em uma sentença que chamamos de equação.
Equações são igualdades, ou seja, nelas aparece o sinal =. Fazendo a solução corretamente, o valor encontrado é a solução da equação.
Equações são como uma balança de dois pratos: você pode tirar ou acrescentar pesos iguais nos dois lados sem alterar o equilíbrio. Veja o exemplo a seguir:
5x + 4 = 2x + 5 [somando –2x em ambos os lados da equação]
5x – 2x = 2x – 2x + 5
3x + 4 = 5
X = 1/3
Do mesmo modo, podemos multiplicar ou dividir os dois lados por um mesmo número, desde que esse número não seja zero.
Exercícios resolvidos
1) Resolva as seguintes equações:
A) 2 + x/3 = 6
B)x/5 + 2 = 3(x – 9) + 1
RESOLUÇÃO
Letra A:
2 + x/3 = 6 [somando –2 em ambos os lados da equação]
X/3 = 4 [multiplicando por 3 ambos os lados da equação]
X = 12
Letra B:
x/5 + 2 = 3(x – 9) + 1 [aplicando a propriedade distributiva]
x/5 + 2 = 3x – 27 + 1 [somando –2 em ambos os lados da equação]
x/5 = 3x – 27 + 1 – 2
x/5 = 3x – 28 [multiplicando ambos os lados da equação por 5]
X = 5.(3x-28)
X = 15x – 140 [somando 140 – x em ambos os lados da equação]
140 = 14X [dividindo ambos os lados da equação por 14]
X = 10
2) Encontre a solução para o problema:
“Há 30 anos eu tinha a terça parte da minha idade atual. Quantos anos eu tenho agora?”
RESOLUÇÃO
Se a idade atual é x, 30 anos atrás era 30 – x. Como esse valor é a terça parte de x, temos a equação:
X – 30 = x/3
3(x – 30) = x
3x – 90 = x
2x = 90
X = 45.
Portanto, a pessoa que formulou o problema deve ter 45 anos.
