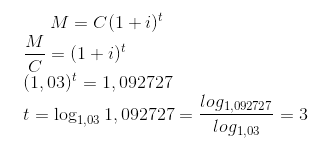Na antiga babilônia, muitas pessoas deixavam seus bens, como cereais e metais preciosos, guardados nos templos. Quando os sacerdotes desses templos emprestavam, por exemplo, sementes de trigo a um agricultor, este deveria devolver as sementes e uma certa quantidade a mais, como uma espécie de juros. Desde aquela época já era empregado um certo juros ao emprestar uma quantidade de algo.
Atualmente, a pessoa que conhece os fundamentos da matemática financeira evita o endividamento, o consumo em época imprópria e o trabalho em excesso para apenas pagar juros, adotando, consequentemente, uma postura consciente em seu papel de consumidor.
Veja, a seguir, como a matemática financeira é utilizada em nosso cotidiano, só aqui, no Gestão Educacional!
Fator de atualização
O fator de atualização (f) é a razão entre dois valores de uma grandeza em tempos diferentes.
Na divisão entre dois valores quaisquer, só existem três resultados possíveis: ou resulta 1, ou maior que 1 ou menor que 1.
Quando o resultado da divisão é 1, os dois valores são iguais, portanto, nenhum é maior nem menor que o outro. Um valor é 100% do outro, por isso dizemos que f = 1 é o fator neutro.
No caso de uma divisão em que o resultado é maior que 1, como A/B = 1,05, podemos entender esse resultado de duas formas diferentes:
- A é 5% maior que B;
- A é 105% de B.
Por fim, quando a divisão resulta em um número menor que 1, por exemplo, A/B = 0,90, podemos entender o resultado de duas maneiras diferentes:
- A é 10% menor que B;
- A é 90% de B.
No caso de escolhermos a primeira opção (A ser maior ou menor que B), podemos calcular a taxa percentual i, a partir do valor do fator de atualização:
- f >1: i = f – 1;
- f < 1: i = 1 – f.
Nos exemplos acima, temos:
- i = 1,05 – 1 = 0,05 = 5%;
- i = 1 – 0,9 = 0,1 = 10%.
Definimos o fator de atualização como:
- Se f > 1, temos um aumento;
- Se f < 1, temos um desconto.
- Se f = 1, não houve mudança no preço.
No caso de aumentos ou descontos sucessivos, podemos calcular o fator acumulado, que é a multiplicação de vários fatores individuais.
Conceitos de matemática financeira
Vamos supor que uma pessoa aplique uma certa quantia (capital) em uma caderneta de poupança por um determinado tempo (período). No fim do período, essa pessoa recebe uma quantia (juros) como compensação. O valor dessa quantia é estabelecido por uma porcentagem, chamada de taxa de juros. No final, a pessoa terá uma quantia que será o capital + juros (montante).
Com esses confeitos definidos, podemos seguir nossos estudos sobre juros.
Juros simples
Se um capital C, aplicado a uma taxa de juros de i% ao período, no sistema de juros simples, rende juros j no fim de um período t, então podemos calcular esses juros e a montante M final com as seguintes fórmulas: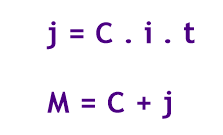
Juros compostos
No sistema de juros compostos, o capital C, aplicado a taxa i ao período, produz juros j e gera um montante M ao fim de t períodos.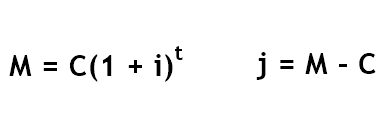
Os valores para juros simples e juros compostos para uma mesma situação são diferentes. Isso ocorre porque no sistema de juros compostos ocorre o que chamamos de “juros sobre juros”, ou seja, o valor do montante do próximo período é calculado de acordo com o montante do período anterior.
Equivalência de taxas
Vamos analisar o seguinte problema:
- Se um investimento rende 3% ao ano, quanto renderá em 10 anos?
i = 3% = 0,03
O montante após 10 anos será dado por: C (1 + 0,3)10.
Se I é a taxa de juros acumulada em 10 anos e i é a taxa de juros relativa a 1 ano, teremos: 1+ I = (1 + i)t.
No nosso problema, temos:
1 + I = (1 + i)t
1 + I = (1 + 0,03)10
1 + I = (1,03)10
I = 0,3439
I = 34,39%
Generalizando, se I é a taxa de crescimento em um período T de tempo e i é a taxa relativa ao período t, temos: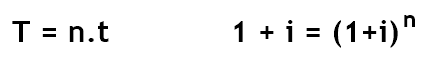
Equivalência de capitais
O valor de uma quantia depende da época da qual ela está referida. Por exemplo, se meu dinheiro rende 1% ao mês, é indiferente pagar R$100,00 agora ou R$101,00 daqui a um mês.
Por outro lado, é mais vantajoso pagar R$100,50 daqui a um mês do que pagar R$100,00 agora. Também é mais vantajoso pagar R$100,00 agora do que R$102,00.
Podemos ler a fórmula Cn = C0(1+i)n da seguinte maneira: uma quantia igual C0 hoje será transformada depois de n períodos de tempo em uma quantia igual a C0(1+i)n a uma taxa de i% de período.
Por exemplo, uma quantia cujo valor atual é 1.000 reais equivalerá no futuro, depois de n períodos de tempo, a 1000(1 + i)n.
Ou seja:
- Para obter o valor futuro, basta multiplicar o atual por (1+i)n;
- Para obter o valor presente, basta dividir o valor futuro por (1+i)n.
Exercícios resolvidos
1) Uma bomba retira em cada sucção 3% de água de um poço. Depois de 20 sucções, quanto restará da água inicialmente existente no poço?
RESPOSTA:
i = -3% = – 0,03
1 + I = (1 – 0,03)20
I ≅ – 0,4563 = – 45,63%
2) Qual deve ser o tempo necessário para que a quantia de R$30.000, 00 gere um montante de R$32.781,81, quando aplicada à taxa de 3% ao mês, no sistema de juros compostos?
RESPOSTA:
