O Mínimo Múltiplo Comum é algo importante dentro da matemática e refere-se a um numero mais próximo de zero e positivo, que é múltiplo, ao mesmo tempo, de dois ou mais números. Ou seja, é o valor mínimo pelo qual dois ou mais números podem ser divididos, resultando em números inteiros.
Para encontrar os múltiplos de um número, basta multiplicá-los pelos números naturais (1,2,3,4,5,6,7,8,9….) e você obterá os resultados. Veja o exemplo, abaixo, para achar os números múltiplos de 3:
- 3 x 1 = 3 ( o resultado 3 é um múltiplo);
- 3 x 2 = 6 ( o resultado 6 é um múltiplo);
- 3 x 3 = 9 ( o resultado 9 é um múltiplo);
- 3 x 4 = 12 ( o resultado 12 é um múltiplo);
- 3 x 5 = 15 ( o resultado 15 é um múltiplo);
- e assim por diante….
Os múltiplos de um número são infinitos, sendo zero um múltiplo de todos os números, afinal, ao multiplicar qualquer número por zero, o resultado sempre será zero. Veja:
- 900 x 0 = 0
- 25 x 0 = 0
- 129 x 0 = 0
Para um número ser múltiplo de outro, é preciso que ele seja divisível por esse número e o resultado seja um número inteiro, ou seja, sem vírgulas. Exemplo:
- 49 é um múltiplo de 7, pois 49 ÷ 7 = 7;
- 25 é um múltiplo de 5, pois 25 ÷ 5 = 5;
- 30 é um múltiplo de 3, pois 30 ÷ 3 = 10.
Calcule o MMC
O MMC pode ser calculado comparando a tabuada de dois números, isso para valores mais baixos. Você deve procurar pelo menor resultado múltiplo que os dois números possuem em comum. Veja o exemplo, para entender melhor, mostrando o MMC de 3 e 5:
Abaixo temos os múltiplos do número três:
- 3 x 1 = 1;
- 3 x 2 = 6;
- 3 x 3 = 9;
- 3 x 4 = 12;
- 3 x 5 = 15.
Agora, os múltiplos do número cinco:
- 5 x 1 = 5;
- 5 x 2 = 10;
- 5 x 3 = 15;
- 5 x 4 = 20;
- 5 x 5 = 25.
A conclusão a que se pode chegar é que o número 15 é o menor múltiplo que 3 e 5 têm em comum, por isso 15 é o MMC entre 3 e 5.
Fatoração
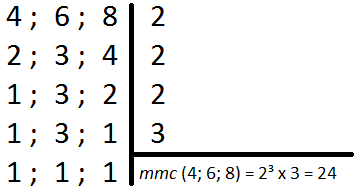O exemplo acima é muito fácil para números menores, porém, quando temos valores maiores, o cálculo não é tão simples assim. Nesses casos, é preciso utilizar a fatoração. A fatoração vai, passo a passo, decompondo os números maiores em números primos ( 2, 3, 5, 7, 11, 17…)
É preciso colocar todos os números lado a lado e começar a dividi-los pelo menor número primo possível. Veja o exemplo utilizando os números 60, 24 e 15 simultaneamente:
- 60 – 24 – 15 | 2 ( divida todos os números possíveis pelo menor número primo);
- 30 – 12 – 15 | 2 (continua sendo o menor número primo divisível);
- 15 – 6 – 15 | 2 (enquanto possível, continue dividindo pelo menor número primo);
- 15 – 3 – 15 | 3 (agora, o menor número primo divisível é 3);
- 5 – 1 – 5 | 5 (a fatoração só para quando todos números chegarem a 1);
- 1 – 1 – 1 | A fatoração acaba aqui, pois todos números chegaram a 1.
Agora, para descobrir o mínimo múltiplo comum, devemos multiplicar todos os números primos que utilizamos na divisão: 2 x 2 x 2 x 3 x 5 = 120. Ou seja, 120 é o mínimo múltiplo comum entre os números 60, 24 e 15.
Agora, é só treinar! Os números primos sempre devem aparecer na lateral, do maior para o menor, se não algo dará errado. O mínimo múltiplo comum entre os números também não pode ser igual a zero.
