Muitas pessoas têm dúvida sobre quais números são irracionais. Por exemplo, todo número decimal é irracional? As dízimas periódicas são números irracionais? Com o objetivo de resolver esse problema e também outros relacionados, você encontrará, neste artigo, o que são os números irracionais, suas propriedades e também os conjuntos.
Os números irracionais são os que não podem ser representados por uma fração. Esses números apareceram a partir de um antigo problema que o filósofo e matemático grego Pitágoras (570 a.C. – 495 a.C.) não queria aceitar, que era o chamado cálculo da diagonal de um quadrado, tendo o lado medindo uma unidade e a diagonal √2. O estudo relacionado a decifrar esse enigma foi responsável pelos primeiros passos de um novo conjunto, que é representado justamente pelos números racionais.
Hoje, você pode pensar o quão fácil é conseguir o valor de √2, basta acessar uma calculadora no celular, tablet ou computador que o resultado é imediato. Mas, imagine determinar isso na época em que os estudos tiveram início, quando a única maneira de obter os valores das raízes quadradas era por meio dos números quadrados, como √2²,√3²,√4² etc. Mais difícil, não?
Com a evolução dos estudos da matemática, os especialistas encontraram outros desafios, como a necessidade do cálculo do comprimento de uma circunferência. Com a realização de incansáveis cálculos, eles perceberam que um número se repetia para qualquer circunferência, sendo denominado, posteriormente, como pi (π). Ele é obtido pela razão do comprimento pelo diâmetro da circunferência, ficando assim:
π = C, ou ainda π = C
d 2r
Exemplos de números irracionais
Vejamos, a seguir, alguns exemplos de números irracionais. É possível perceber que a parte decimal não possui qualquer estrutura que possa ser representada por uma fração, assim como costuma ocorrer nas frações periódicas.
Constantes irracionais ou números transcendentais:
- π = 3,1415926535897932384… (Número pi, constante de Arquimedes);
- φ = 1,61803398874989… (número áureo ou número de ouro);
- e = 2,7182818… (Constante de Euler).
Números irracionais obtidos pela raiz quadrada de um número:
- √2 = 1,4142135623730950488016887242097…
- √3 = 1,7320508075688772935274463415059…
- √5 = 2,236067977499…
- √7 = 2,645751311064…
Ou seja, os números irracionais são aqueles em que nunca saberemos o valor da última casa decimal, isso porque eles são números decimais infinitos e não periódicos, isto é, existem infinitas casas decimais, sendo que nenhuma delas ocorre em um período de repetição.
Números irracionais e dízimas periódicas
Vale destacar um item para falar das diferenças entre os números irracionais e as dízimas periódicas, isso porque as dízimas são números racionais. Ainda que elas apresentem uma representação decimal infinita, podem ser representadas pelas frações.
A diferença para os irracionais é que a dízima periódica apresenta um período, isto é, tem sempre a mesma sequência de repetição. Um exemplo disso é o caso do número 0,3333… que pode ser escrito por meio de uma fração denominada irredutível, dessa forma:
0,33333… = 1
3
Sendo assim, as dízimas periódicas não são números irracionais.
Classificação dos números irracionais
Os números irracionais podem ser classificados como algébricos ou transcendentes. No primeiro caso, assim o será quando satisfaz uma equação algébrica de coeficientes inteiros. Quando não for o caso, é considerado transcendente.
Como exemplo podemos citar a raiz quadrada de 2 (√2), que pode ser escrita como x2 – 2 = 0, ou seja, é um irracional algébrico.
Um dos números transcendentais mais famosos é o pi (π). Seu valor é π = 3,14159265358979323846…, o que representa a proporção da medida da circunferência e seu diâmetro. Outro caso de número irracional transcendente é o número de Neper, representado por e, cujo valor aproximado é igual a 2,718281.
Ainda, há o número de ouro, representado por Phi (ϕ). Seu valor é ϕ = 1,618033… Neste caso, o número de ouro é localizado a partir da razão áurea ou divina da proporção, sendo facilmente achado em vários elementos da natureza. Essa razão se faz presente em muitas pinturas, esculturas e construções arquitetônicas ao longo da história de nossa civilização.
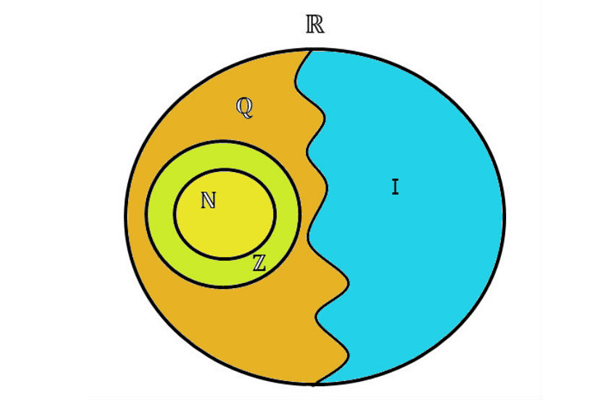
Por fim, vale dizer que o conjunto dos números irracionais é representado pela letra I maiúscula. A união desse conjunto com o conjunto dos números racionais, representados pela letra Q, levam ao conjunto de números reais (R). Os números irracionais possuem elementos infinitos e, por isso, são em maior quantidade do que os racionais.
