Em nosso cotidiano, é ideal tentar representar figuras tridimensionais em um plano. Um exemplo disso são os mapas, que representam regiões do nosso planeta em um pedaço de papel.
O plano cartesiano é um modo de facilitar a localização de pontos, figuras, entre outros objetos. Estudaremos, a seguir, o que ele é e como utiliza-lo.
Retas numéricas do plano cartesiano
Nas estradas, os marcos quilométricos ajudam na localização, constituindo um referencial, isto é, um marco para indicar a posição de pessoas, veículos e lugares ao longo de uma estrada.
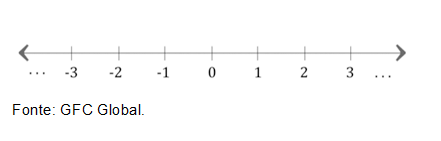
Na matemática, as retas numéricas são similares às estradas com marcos quilométricos. Os pontos da reta podem ser localizados pelos números associados a eles, como mostra a figura abaixo.
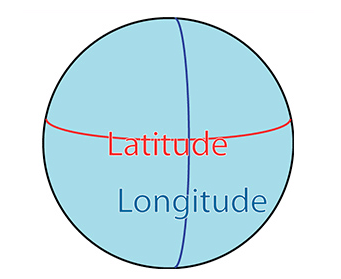
Nos mapas, são desenhadas linhas horizontais (que marcam as latitudes) e linhas verticais (que marcam as longitudes), indicadas por medidas em grau. Isso auxilia a identificar com precisão cidades, embarcações, oceanos, etc.
Nossa capital, Brasília, está situada, aproximadamente, na latitude 16° sul (linha horizontal) e na longitude 48° oeste (linha vertical). Essas indicações são as coordenadas geográficas do lugar.
Um dos primeiros estudiosos a pensar nesse referencial foi o matemático Claudio Ptolomeu, que viveu entre os anos 90 e 168, no século II.
Na matemática, para localizar dois pontos no plano, usamos um referencial parecido com os das coordenadas geográficas.
Plano cartesiano
Primeiro, vamos traçar duas retas numeradas, perpendiculares entre si, ou seja, elas formam um ângulo reto (ângulo de 90°). Vamos chamar elas de eixo horizontal de coordenadas e eixo vertical de coordenadas.
Os eixos cortam-se no ponto O, que recebe o nome de origem, correspondendo ao zero de cada eixo.
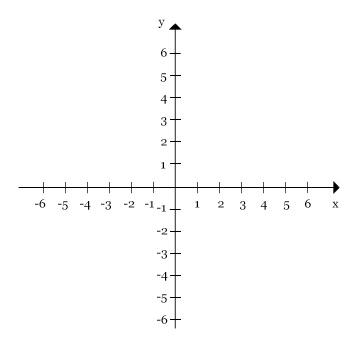
Denominamos o eixo horizontal de eixo x, que é o eixo das abscissas. Enquanto isso, o eixo vertical chamado de eixo Y é o eixo das ordenadas.
O plano cartesiano se estende infinitamente, por isso, colocamos flechas para mostrar que a reta continua além do nosso desenho.
Como localizar um ponto no plano cartesiano?
Observe a imagem abaixo. Vamos definir o ponto O, que está em laranja, como a origem. Ele possui coordenadas (0,0).

Vamos localizar as coordenadas do ponto A que está em vermelho. Partimos da origem O em laranja e seguimos primeiro na horizontal, andando 3 unidades para a esquerda e uma unidade para cima, ou seja, seguimos primeiro na horizontal e depois na vertical. Obtemos, então, os números -3 e 1, que são as coordenadas geográficas do ponto A.
Para achar as coordenadas do ponto B, andamos duas unidades para a direita e depois três unidades para cima. Obtemos os números 2 e 3, que são as coordenadas do ponto B.
Perceba, todas as posições no plano cartesiano são medidas em relação a ponto de origem.
Para evitar confusão, os números das coordenadas devem ser apresentados sempre nessa ordem: primeiro o avanço horizontal, depois o vertical.
Nesse caso, como andamos para a esquerda no eixo X, estamos andando no sentido negativo. Quando tentamos achar as coordenadas do ponto B, andamos no sentido positivo.
Com isso, podemos perceber que a localização de um ponto é dada por suas coordenadas que são representadas por um par de números entre parênteses.
O primeiro valor é correspondente à posição de um ponto em realização ao eixo das abcissas; já o segundo número entre os parênteses é referente ao eixo das ordenadas.
Portanto, os pontos A e B podem ser escritos como A (-3, 1) e B (2,3).
De modo análogo, podemos ver que o ponto C está nas coordenadas (-1,-2). Isso ocorre porque vamos andar para baixo, para encontrar a coordenada em Y.
De modo genérico, os pontos são descritos como: P (x,y).
Quadrantes do plano cartesiano
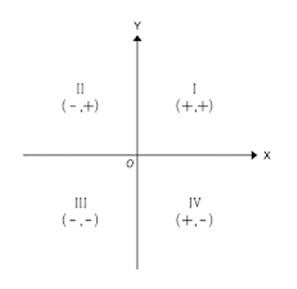
Existem quatro quadrantes que dividem o plano cartesiano: I, II, III e IV.
A identificação de cada quadrante segue o sentido anti-horário a partir da definição do primeiro quadrante, como mostra a imagem abaixo:
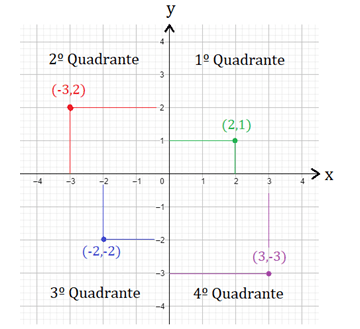
Como pode ver, o ponto verde está no primeiro quadrante, o vermelho no segundo, o azul no terceiro e o roxo no quarto.
Podemos estudar os sinais dos pontos em cada quadrante da seguinte forma:
- Todo ponto do primeiro quadrante tem as coordenadas em x e em y positivas, de modo geral: (x,y).
- Todo ponto do segundo quadrante tem as coordenadas no eixo x negativas e no eixo y positivas, de modo geral: (-x, y).
- Todo ponto do terceiro quadrante tem ambas as coordenadas negativas, de modo geral: (-x, -y)
- Todo quarto quadrante apenas as coordenadas do eixo Y são negativas. De modo geral: (x, -y).
Podemos observar isso na figura abaixo: