A probabilidade é o ramo da matemática que cria e pesquisa modelos para estudar fenômenos aleatórios. Cálculos que mostram a probabilidade de um evento informam quais são as chances desse evento ocorrer em uma determinada situação.
A noção de probabilidade foi construída de pouco em pouco. Ela nasceu relacionada à observação de resultados de jogos de azar e ao surgimento do seguro contra perdas. Já o cálculo sistemático de probabilidade iniciou no século XVI e XVII, com os matemáticos Girolamo Cardamo e Galileu Galilei.
Da previsão do tempo ao lançamento de uma nave espacial, a probabilidade quantifica as incertezas, possibilitando que se crie estratégias para a redução de falhas e alcance de melhores resultados. Essa área é usada na engenharia, economia, biologia, psicologia, física, entre outras. A seguir, conheça mais sobre probabilidade e possibilidade, só aqui, no Gestão Educacional!
Probabilidade: espaço amostral e evento
Há certos fenômenos que, embora sejam feitos em condições idênticas, não apresentam o mesmo resultado, como é o exemplo de jogar um dado duas vezes. Como não sabemos o resultado exato de um evento, buscamos quais são as chances, a probabilidade, de ele ocorrer.
Em um certo evento, o conjunto formado por todos os resultados possíveis é chamado espaço amostral (Ω). Qualquer subconjunto do espaço amostral é chamado de evento.
Geralmente, procuramos eventos favoráveis nesse espaço amostral, ou seja, situações em que ocorrem o que queremos ou procuramos. Esses são os resultados favoráveis.
Calculo da probabilidade
Dizemos que a probabilidade é a razão entre o número de casos favoráveis e o número de resultados possíveis.
Ou seja, estamos procurando quais são as chances de um evento A ocorrer em todos os resultados possíveis.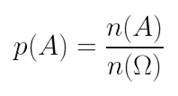 Em outras palavras, a probabilidade de um evento A ocorrer é dada pela divisão do número de elementos de A (evento favorável) pelo número total de possibilidades.
Em outras palavras, a probabilidade de um evento A ocorrer é dada pela divisão do número de elementos de A (evento favorável) pelo número total de possibilidades.
Evento certo, incerto e mutuamente exclusivo
Vamos imaginar o seguinte exemplo:
Quando jogamos um dado, temos 6 possibilidades de resultado: 1, 2, 3, 4, 5, 6. Portanto, nosso espaço amostral será: Ω = {1, 2, 3, 4, 5, 6}.
Agora, queremos saber qual é a probabilidade de obtermos um número par quando jogarmos esse dado.
Os casos favoráveis serão: A = {2, 4, 6}.
Calculando a probabilidade, temos:
- P(A) = 3/6 = ½ = 50% de chance.
Agora, vamos observar quais são as chances de ocorrer:
- Evento A – ocorrência de um número menor que 7: A = {1, 2, 3, 4, 5, 6, 7}. Portanto A = Ω
Quando o evento coincide com o espaço amostral, chamamos ele de evento certo.
- Evento B – ocorrência de um número maior que 6. Portanto B = Ø.
Quando um evento é vazio, chamamos ele de evento impossível.
A probabilidade assume valores de 0 a 1. Quando p(A) = 0, o evento A é impossível. Quando p(A) = 1, o evento A é evento certo, e há certeza de que ele ocorrerá.
Probabilidade da união de dois eventos e evento complementar
Chamamos de Ā a notação para complementar um evento A.
Temos:
- Ā U A = Ω
- Ā ∩ A = Ø
Portanto, definimos que:
- P(Ā) = 1 – P(A)
(Para ver um exemplo, vá até o exercício resolvido 2).
Se conhecemos quais são as probabilidades de ocorrer um evento A e um evento B, a probabilidade de ocorrer os dois, ou seja, p(A U B), é dada por:
- P(A U B) = p(A) + p(B) – p(A ∩ B)
Exercícios resolvidos
1) Consideramos o experimento aleatório do lançamento de uma moeda perfeita. Qual a probabilidade de sair cara?
RESPOSTA:
Ao jogar uma moeda, temos duas opções de resultado: cara (C) ou coroa (C’). Portanto, nosso espaço amostral será:
Espaço amostral Ω = {C, C’} = 2
Evento A: ocorrência de cara A = {C} = 1
Calculando a probabilidade:
P(A) = ½ = 50% de probabilidade de sair cara.
2) No lançamento simultâneo de dois dados perfeitos, qual é a probabilidade de não sair soma 5?
RESPOSTA:
Nesse caso, veremos que o espaço amostral Ω = 36
Ω = {(1,1), (1,2), (1,3), … (6,5), (6,6)}.
Seja A o evento “sair soma 5”.
A = {(1,4), (2,3), (3,2(, (4,1)} = 4
Calculando a probabilidade de A:
P(A) = 4/36 = 1/9
O evento Ā é o evento não sair soma 5. Justamente o que queremos. Portanto:
P(Ā) = 1 – p(A)
P(Ā) = 1 – (1/9) = 8/9
A probabilidade de não sair soma 5 é 8/9.





