Polígonos são uma linha fechada formada apenas por seguimentos de reta do mesmo plano que não se cruzam. Em nosso dia a dia, sempre estamos em contato com várias formas poligonais, até mesmo quando não percebemos.
A seguir, faremos um estudo sobre o que são polígonos e quais são as suas propriedades.
Polígonos convexos e não convexos
Se marcamos um seguimento de reta dentro de uma região poligonal, podemos encontrar duas situações:
- O seguimento estar totalmente contido dentro do polígono;
- O seguimento não estar inteiramente contido nesse polígono.
Caso o seguimento esteja totalmente contido, temos um exemplo de polígono convexo. Caso isso não ocorra, temos então um polígono não convexo.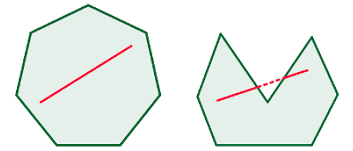
A figura da esquerda é um polígono convexo. Já a figura da direita é um polígono não convexo.
Elementos de um polígono convexo
Em um polígono convexo, temos:
- Vértices;
- Lados;
- Diagonais (seguimentos que ligam um vértice a outro vértice não consecutivo a ele);
- Ângulos externos;
- Ângulos internos.
Em qualquer polígono convexo, o número de vértices, lados, ângulos internos e ângulos externos será igual.
Polígono regular
Um polígono convexo é denominado polígono regular quando todos os seus lados são congruentes e todos os seus ângulos internos são também congruentes.
O nome dos polígonos regulares é determinado de acordo com o seu número de lados. Por exemplo: triângulo (tri = 3) possui três lados. Abaixo, veja exemplos de polígonos regulares e seus respectivos nomes de acordo com os números de lados: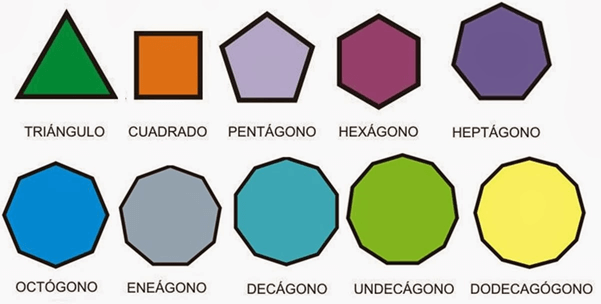
Soma das medidas dos ângulos externos de um polígono convexo
Em qualquer polígono convexo, a soma das medidas dos ângulos externos é igual a 360°.
Sendo Se a soma dos ângulos externos, podemos escrever: Se= 360º.
Soma das medidas dos ângulos internos de um polígono convexo
No triângulo, a soma dos ângulos internos é igual a 180°.
Quando acrescentamos mais um lado em um polígono, estamos praticamente adicionando um triângulo a essa figura. Veja a imagem abaixo: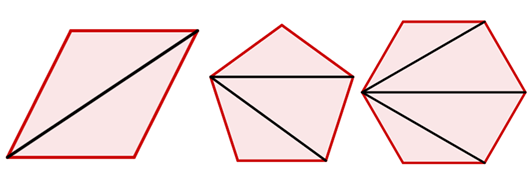
Podemos formar um polígono de 4 lados com dois triângulos. Portanto, a soma S dos ângulos internos será:
- Si = 2. 180° = 360°
Para formar um polígono de 5 lados, utilizamos três triângulos.
- Si = 3. 180 = 540°
Para formar um polígono de 5, utilizamos 4 triângulos.
- Si = 4. 180° = 720°
De modo geral, se o polígono tem n lados, a soma Si das medidas dos ângulos internos é dada por: Si= (n-2) . 180º.
Ângulos internos em polígonos regulares
Sendo ai a medida de cada ângulo interno em um polígono regular, podemos encontrar esse valor a partir do seu número de lados (n) com a seguinte fórmula: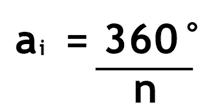
Por exemplo, em um triângulo equilátero, teremos:
- N = 3 lados.
- ai = 360°/3 = 120°.
Número de diagonais de um polígono
Cada vértice de um polígono de n lados tem n – 3 diagonais, já que diagonais podem ser ligadas a todos os outros vértices, exceto aos dois consecutivos e a ele próprio.
Cada vértice do polígono, então, possui n – 3 diagonais. Como o número de lados em um polígono convexo é igual ao seu número de vértices, podemos dizer que um polígono de n lados tem n diagonais.
O número de diagonais poderia ser dado, então, multiplicado (n-3) pelo número de vértices do polígono. Porém, se fizermos isso, estamos contando cada diagonal duas vezes. Temos que dividir esse valor por 2.
Por fim, a fórmula para calcular o número de diagonais de um polígono convexo é: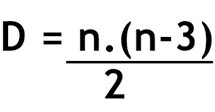
Outras propriedades dos polígonos regulares
- O eixo de simetria divide o polígono em duas partes simétricas (iguais).
Todos os polígonos regulares podem ser girados em torno de um eixo de simetria, e ele ainda será igual.
- Todo polígono regular pode ser circunscrito por um círculo que toca todos os seus vértices, como mostra a imagem abaixo;
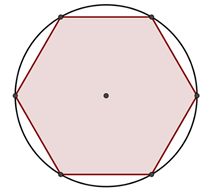
- Todo polígono regular tem um círculo inscrito, ou seja, um círculo que toca os pontos médios de cada lado, como mostra a imagem abaixo.
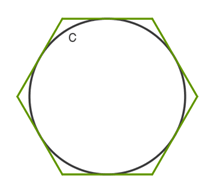
Exercícios Resolvidos
1) Responda:
A) Quantos vértices tem um dodecágono?
B) Qual o polígono convexo que tem o número de lados igual ao número de diagonais?
RESPOSTA:
A) Um dodecágono tem 12 lados, pois um polígono é nomeado de acordo com seu número de lados. Consequentemente, ele tem 12 vértices, pois o número de lados é igual ao número de vértices em um polígono convexo.
B) O pentágono. Ele possui 5 lados e 5 diagonais.
