A área de figuras planas é um importante conceito que estudamos durante o ensino fundamental. Esses conhecimentos serão usados mais adiante em problemas do ensino médio, como o cálculo da velocidade média a partir da área abaixo do gráfico, tempo x espaço, entre outras situações.
O quadrado é uma figura plana que possui quatro lados iguais, ou seja, quatro lados que possuem a mesma medida. Ele também conta com quatro ângulos internos retos (ângulos de 90°). Veremos, a seguir, como efetuar o cálculo de área, que é feito pela fórmula A = l², sendo l a medida do lado.

O que é área?
Primeiramente, vamos definir o que é a área de uma região.
Dizemos que a área de um local é a quantidade de espaço que está contido nele. Para medirmos essa quantidade, usamos unidades de medida.
As unidades de medida mais utilizadas no cálculo de áreas são centímetros quadrados (cm²) e metros quadrados (m²).
Para imaginar o que é 1cm² e 1m², observe a figura abaixo:
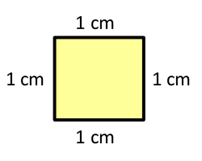
Chamamos de centímetro quadrado a unidade de área que representa um quadrado com 1cm de lado:
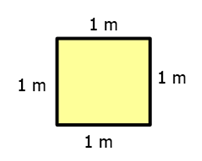
De modo análogo, chamamos de metro quadrado a unidade de área que representa um quadrado com 1m de lado. Com isso, podemos utilizar esse conceito para imaginar como calcular a área de uma região.
Como calcular a área de um quadrado?
Observe a figura abaixo:
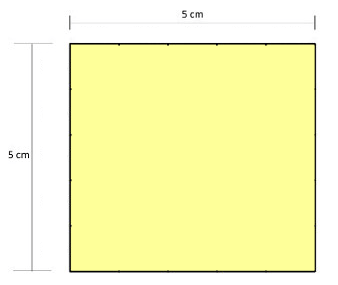
Temos uma região quadrada em que a medida dos seus lados é de 5cm. Para calcular sua área, podemos imaginar que vamos preencher essa região com vários quadradinhos que valem 1cm².
Obteremos, como resultado disso, algo parecido com a figura abaixo:
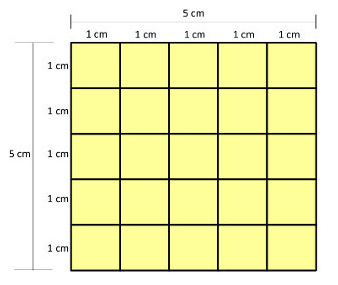
Se você contar quantos quadradinhos utilizou, verá que foram usados 25 ao todo, ou seja, esse quadrado maior possui 25 centímetros quadrados dentro dele. Porém, existe outro modo de descobrir isso de maneira muito mais rápida.
Basta multiplicar a 5 cm por 5 cm = 25 cm², o que fizemos acima por multiplicar a medida de seus lados. Generalizando, podemos finalmente escrever a área do quadrado como:
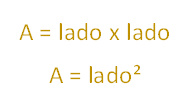
Chamando a medida do lado de L, teremos:
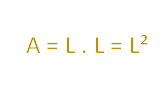
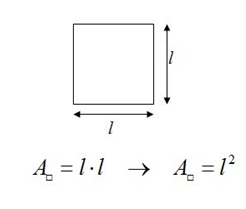
Unidades de medida
Sempre que obtermos um valor para a área, devemos incluir logo ao lado a unidade de medida. Se o quadrado tem a medida dos seus lados em centímetros, a área será dada em cm². Se o quadrado é medido em metros, a área será dada em m².
Portanto, a unidade de medida para a área sempre estará ao quadrado.
Exercícios Resolvidos
1) Sabendo que a medida da lateral de um quadrado é dada por 5 metros, calcule a sua área.
RESPOSTA: A = L² = 5² = 25 m²
2) O quadrado maior é composto por 3 quadrados médios azuis e 4 quadrados pequenos amarelos, como mostra a imagem abaixo.
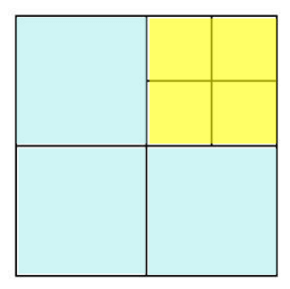
Sabendo que o quadrado médio azul possui a medida lateral de 4cm e o quadrado pequeno amarelo possui a medida da sua lateral igual à metade da lateral do quadrado azul, calcule a área total do quadrado maior.
RESPOSTA:
Lateral do quadrado pequeno = 4/2 = 2.
Calculando a área do quadrado amarelo, teremos:
A(amarelo) = 2×2 = 4 cm².
Como são 4 quadrados amarelos, teremos: 4×4 = 16 cm².
Calculando a área de 1 quadrado azul:
A(azul)= 4² = 16 cm².
Como temos 3 quadrados azuis: 3 x 16 = 48 cm².
Somando os valores obtidos para calcular a área do quadrado maior:
16 cm² + 48 cm² = 64 cm².





