O cálculo da área de determinadas figuras planas nos auxilia em algumas atividades, por exemplo, durante a compra de um terreno. Se queremos um terreno grande para construir um estacionamento de um shopping, utilizamos o conceito de área para escolher qual comprar. Por exemplo, sem esse estudo, poderíamos acabar comprando um terreno de 20m², que pode ser pequeno para o que precisamos.
A área de um determinado local representa a quantidade de espaço que essa superfície tem. Utilizamos sempre uma unidade de medida para representar esse valor, que pode ser metros quadrados (m²), centímetros quadrados (cm²), e assim por diante.
A seguir, vamos discutir a seguir a área de figuras planas, ou seja, a área de figuras que possuem duas dimensões: altura e largura. Confira essas e outras informações completas só aqui, no Quero Viver Bem!

[VEJA TAMBÉM: ÁREA E PERÍMETRO – QUANDO USAMOS?]
Área do quadrado
Uma unidade de área muito usada é o centímetro quadrado. Para visualizar essa unidade, pense em um quadrado com cada lado de medida igual a 1cm, como mostra a figura, abaixo.
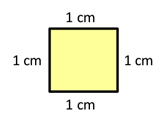
Quando dizemos que um quadrado tem 9cm² de área, estamos afirmando que existem 9 quadradinhos como esse acima dentro do quadrado maior. Veja a representação disso na figura, abaixo.
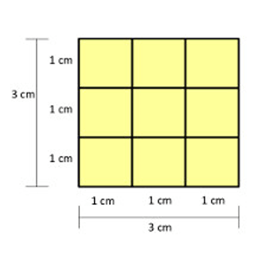
Para calcular a área dessa região, multiplicamos a medida dos seus lados: 3 x 3 = 9cm².
Portanto, a área do quadrado é: A = lado x lado = lado².
Área do retângulo
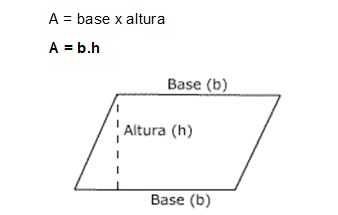
Do mesmo modo, podemos calcular a área do retângulo multiplicando o tamanho da sua base pela sua altura. Isso também irá nos mostrar quantos quadradinhos existem dentro do retângulo.
Sendo b a medida da base e h a medida da altura, teremos:
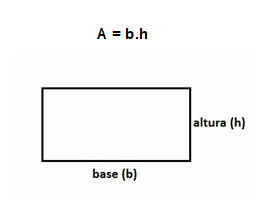
Área do paralelogramo
O paralelogramo é o quadrilátero no qual os seus lados opostos são paralelos.
Para calcularmos a área da região plana limitada pelo paralelogramo ABCD, podemos pensar da seguinte maneira:
Observe a imagem abaixo, traçando linhas pontilhadas, podemos ver dentro do paralelogramo um triangulo de vértices ADF, que está pintado em azul.
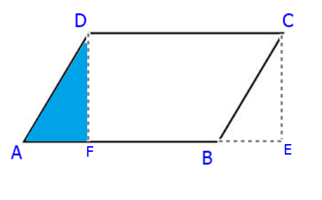
Se deslocarmos esse triangulo azul para a direita, ele consegue completar um retângulo, como o mostrado em azul claro, abaixo.
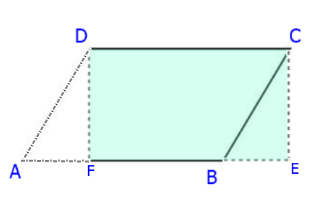
Assim, podemos pensar que, para calcular a área do paralelogramo, basta multiplicar a medida de sua base pela altura.
Área do triângulo
O triângulo é uma figura plana que possui 3 lados e a soma dos seus ângulos internos é 180°.
Conhecendo a área do paralelogramo, podemos enfim determinar a área do triângulo.
Considere um paralelogramo como dois triângulos juntos, como mostra a figura abaixo.
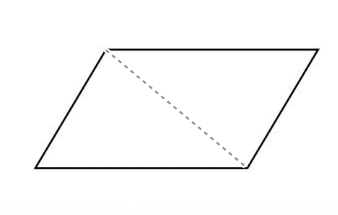
Para calcular a área do triângulo, basta dividir a área do paralelogramo por 2 – A = b.h / 2.
Essa formula acima pode também ser usada para o cálculo da área de triângulos retângulos, que são triângulos que possuem um ângulo reto, ou seja, um ângulo que mede 90°.
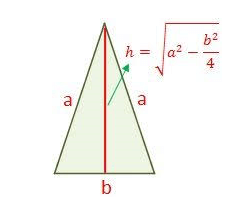
Também usamos a fórmula acima para calcular a área de triângulos que possuem apenas dois lados de mesma medida, chamamos de triângulo isósceles.
Nesse caso, para descobrir sua altura, devemos fazer o Teorema de Pitágoras, como mostra a figura, abaixo:
Chamamos de triângulos escalenos aqueles que possuem os três lados com medidas diferentes. Quando sabemos o valor de um dos ângulos internos desse triângulo, a formula, a seguir, é utilizada:
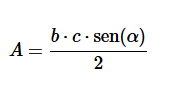
Sendo b, c e o ângulo α mostrados na figura.
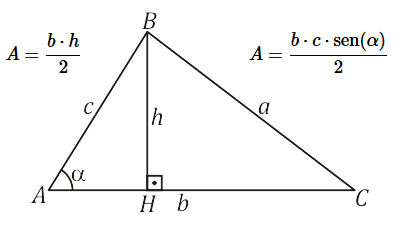
Chamamos de triângulos equiláteros aqueles que possuem os 3 lados de mesma medida. Para esse caso, podemos usar a seguinte fórmula:
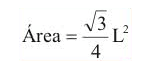
Área do losango
Um losango é uma figura plana onde seus 4 lados possuem a mesma medida, porém, nenhum de seus ângulos é reto.
Dizemos que a área de uma região determinada por um losango é igual à metade do produto das medidas de suas diagonais.
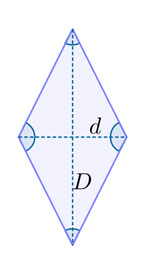
Sendo sua área dada então por:
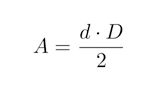
Área do trapézio
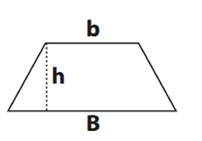
O trapézio é uma figura plana que possui quatro lados, sendo 2 deles paralelos entre si, como mostra a figura, a seguir.
Podemos calcular a sua área seguindo a fórmula:
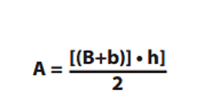
Área de polígonos regulares
Polígonos regulares podem ter um número diverso de lados. Existem polígonos de 6 lados (como o hexágono), polígonos de 5 lados chamados de pentágono, etc.
Para calcularmos a área de figuras assim, primeiro precisamos calcular a medida de seu apótema.
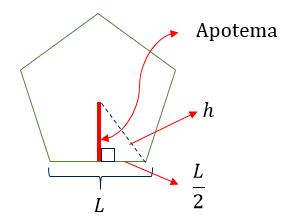
Para isso, podemos também utilizar o Teorema de Pitágoras, obtendo, então, a seguinte fórmula:
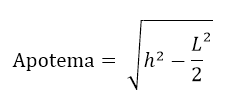
Sendo L a medida dos lados do polígono.
Com isso, finalmente pode ser calculada a área de qualquer polígono regular – A = (a . p) / 2, sendo a = medida da apótema do polígono regular; p = perímetro do polígono regular.
Exercícios Resolvidos
1) Determine a área de uma região do plano que tem a forma de um paralelogramo, cuja base mede 7,5cm e a altura correspondente a 2,1cm.
RESPOSTA: A = b. h = 7,5 . 2,1 = 15,75 cm²
2) A área de um sítio retangular é de 414 200 m². O comprimento desse sítio mede 760m. Quanto mede sua largura?
RESPOSTA:
A = b.h
414 200 = 760 . h
h = 545 m.





