Primeiramente, vamos definir que grandeza é algo que pode ser medido. Ou seja, comprimento, temperatura, tempo, massa e área são grandezas.
Existem grandezas que são diretamente proporcionais, inversamente proporcionais e grandezas não proporcionais. Para entender esses conceitos, vamos estudar grandezas diferentes e suas proporcionalidades.
Proporcionalidade direta
Se duas grandezas são diretamente proporcionais, quando o valor da primeira é multiplicado por um número positivo, o valor da segunda também será multiplicado pelo mesmo número. Por exemplo:
1) O preço de frutas costuma ser diretamente proporcional ao número de frutas comprado. Se você vai ao supermercado, quanto mais maçãs você comprar, maior será o valor da sua compra.
Sabendo o preço de 3 maçãs, podemos encontrar o preço de 12 maçãs.
Primeiro, vamos organizar as informações do enunciado:
- 3 maçãs = R$5,00;
- 12 maçãs = ?.
Note que, de 3 para 12, o número 3 foi multiplicado por 4. Para encontrar esse número 4, basta fazer mentalmente 12 ÷ 3 = 4.
Como o número de maças é diretamente proporcional ao preço, basta também multiplicar o valor de 5 reais por 5.
Preço: 5 . 4 = 20 reais.
Concluímos, então, que o preço de 12 maçãs é igual a R$20,00.
Vamos analisar outro exemplo:
2) Certo helicóptero pode percorrer 150 quilômetros em 0,5 hora. Mantendo essa velocidade, quantos quilômetros ele percorrerá em duas horas?
Aqui, o tempo gasto é diretamente proporcional à distância percorrida, ou seja, se o tempo dobrar, a distância também dobra; se o tempo triplicar, a distância também triplica.
Perceba: existe uma relação entre as duas grandezas. Se o tempo gasto for multiplicado por determinado número, a distância percorrida será multiplicada pelo mesmo número.
Para saber a distância percorrida em duas horas, basta fazer:
- 2 ÷ 0,5 = 4;
- 140 . 4 =
Completando a tabela, temos:
Em tabelas com duas grandezas proporcionais, há relações multiplicativas tanto na “vertical” (como fizemos acima) quanto na “horizontal” (como vamos fazer no exercício resolvido, abaixo).
Exercício resolvido
1) Para fazer 6 bengalas de pão, o padeiro utiliza 1.800 gramas de farinha. Quanto ele gasta para fazer 5 bengalas?
RESPOSTA:
Temos que:
- 6 bengalas = 1.800g de farinha;
- 5 bengalas = ?.
É difícil, nesse caso, relacionar o número 5 com 6. Porém, podemos perceber que, ao multiplicar 6 por 300, obtemos 1.800 (6 . 300 = 1.800).
Portanto, para encontrar a quantidade de farinha necessária para fazer 5 bengalas, vamos também multiplicar 5 por 300.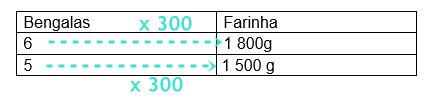
Nesse caso, fizemos uma multiplicação “na horizontal”. Essa também é uma maneira de resolver exercícios.
Grandezas não proporcionais
Devemos ter agora um pouco de atenção, pois nem sempre há proporcionalidade em uma situação. Vamos analisar o seguinte exemplo:
1) Em um jogo de futebol, caso o tempo de jogo triplique de 30 minutos para 90 minutos, o placar não irá obrigatoriamente triplicar também. Isso ocorre porque o tempo de jogo e o placar não são grandezas proporcionais.
Outro exemplo:
2) Nesse ano, você foi 5 vezes ao parque. No ano que vem, a quantidade de anos em questão irá dobrar, mas a quantidade de vezes que você irá ao parque pode ser maior ou menor que 10. Não podemos usar a matemática para prever quantas vezes você irá ao parque.
Grandezas inversamente proporcionais
Se duas grandezas são inversamente proporcionais, quando o valor da primeira é multiplicado por um número positivo n, o valor da segunda é dividido por n (ou seja, seria o mesmo que multiplicar por 1/n). Exemplo:
1) O tempo de duração de uma viagem varia de acordo com a velocidade média de um veículo.
- 50km/h (velocidade média) = 100;
- 3 horas (tempo de viagem) = ?.
Duplicando a velocidade média do veículo, saímos de 50km/h para 100km/h. Portanto, multiplicamos 50 por 2.
Para descobrir o tempo de viagem, vamos dividir 3 por 2, obtendo que o tempo de viagem cai para 1,5h.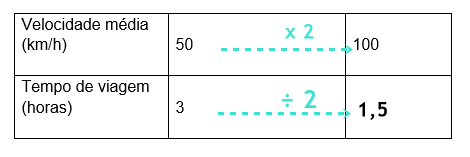
Aplicações da proporcionalidade
1) A escala de um mapa ou de uma planta indica a proporção (ou a razão) entre os comprimentos da representação e os comprimentos da realidade;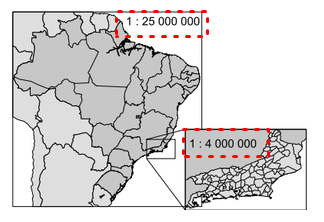
2) Nos gráficos de setores, as medidas dos ângulos de cada setor são proporcionais às quantidades representadas em cada um;
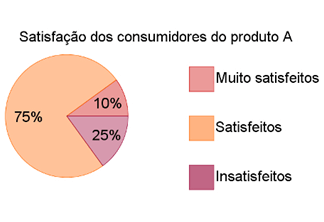3) Nas pesquisas estatísticas, supõe-se que os resultados obtidos no grupo pesquisado (amostra) sejam proporcionais aos resultados que seriam obtidos se toda a população fosse pesquisada.
