Quando realizamos certos cálculos algébricos na dedução de fórmulas, resoluções de equações, entre outras situações, precisamos realizar diversas operações. O processo de fatoração nos ajuda a simplificar expressões, mas nem sempre conseguimos fugir de multiplicar polinômios.
Algumas dessas multiplicações são chamadas de produtos notáveis, que são multiplicações entre polinômios que aparecem com muita frequência em expressões algébricas. A seguir, conheça os principais produtos notáveis e como utilizá-los em exercícios.
Quadrado da soma de dois termos
Quando temos algo do tipo (a + b)², podemos aplicar a propriedade distributiva da multiplicação, que conhecemos popularmente como “chuveirinho”.
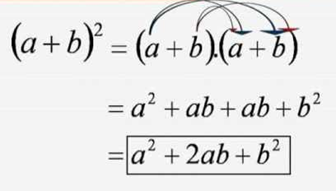
Com isso, obtemos o produto notável (a² + 2ab + c²) que é chamado trinômio quadrado perfeito. Para visualizar isso geometricamente, vamos pensar da seguinte maneira: imagine um quadrado de lados a (quadrado azul).
Junto com esse quadrado, vamos colocar dois retângulos com as medidas dos seus lados iguais a e b (retangulos lilas).
Por fim, também vamos adicionar um quadrado de lado b (quadrado rosa), da maneira como mostra a figura abaixo: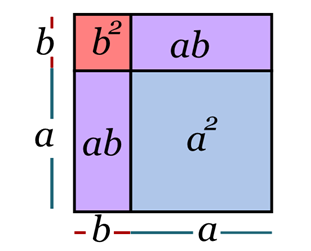
O lado do quadrado maior, formado pelas figuras que citamos acima, mede (a+b). Para encontrar a área desse quadrado, temos que somar a área das quatro figuras que formam o quadrado maior.
Ou, por um segundo método, podemos multiplicar a medida dos seus lados, fazendo (a+b).(a+b) = (a+b)².
- Calculando a área pelo primeiro método:
O quadrado azul tem área A1 = a².
Os retângulos lilás têm área A2 = ab.
O quadrado rosa tem área A3 = b².
Somando essas áreas, temos: a² + ab + ab + b² = a² + 2ab + b²
- Calculando a área pelo segundo método:
- (a + b)² = a² + 2ab + b²
Perceba: ambos deram o mesmo resultado!
Para entender melhor, assista o seguinte vídeo:
Quadrado da diferença de dois termos
Essa multiplicação é parecida com a anterior. Porém, ao invés da soma, temos uma diferença: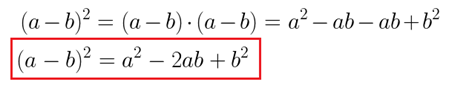
O resultado obtido (a² – 2ab + b²) também é conhecido como trinômio quadrado perfeito. Nesse caso, ele é o quadrado de uma diferença.
Produto da soma pela diferença de dois termos
São exemplos multiplicações do tipo (a + b).(a – b) ou (x + 3) (x – 3).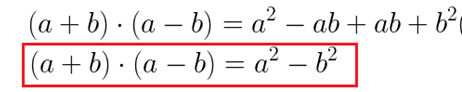
Esses são os três principais produtos notáveis que usamos em expressões algébricas. A seguir, conheça outros produtos notáveis que também possuem relevância.
Cubo da soma
Nesse caso, temos a seguinte multiplicação: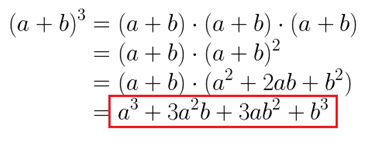
Portanto, sempre que virmos em expressões algébricas o cubo da soma, podemos usar o seguinte produto notável: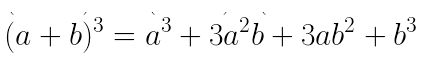
Cubo da diferença
Nesse caso, iremos fazer a seguinte multiplicação: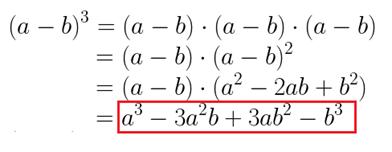
Portanto, sempre que vimos em expressões algébricas o cubo da diferença, podemos substituir por: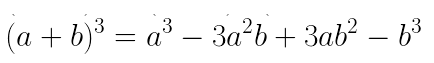
Resumo produtos notáveis
Assim, podemos montar um pequeno resumo dos produtos notáveis mais utilizados: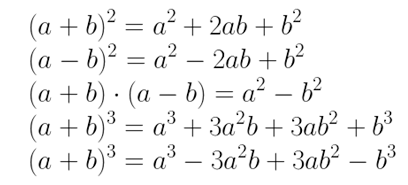
Exercícios resolvidos
1) Efetue as seguintes operações:
A) (x – 4)²
B) (2x – 5)(2x + 5)
C) (3x + 1)²
RESPOSTA:
A) Nesse caso, temos o quadrado de uma diferença. Usaremos então: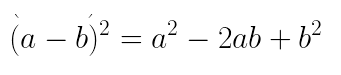
Portanto, temos:
(x – 4)² = x² -2.4x + 4² = x² -8x + 16
B) No item B, estamos lidando com o produto da soma pela diferença de dois termos. Usaremos o seguinte produto notável: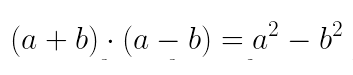
Portanto, temos:
(2x – 5) (2x + 5) = (2x)² – 5² = 4x² – 25
C) Temos, nesse item, o quadrado de uma soma. Usaremos, então, o seguinte produto notável: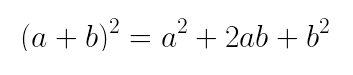
Portanto, temos:
(3x +1)² = (3x)² + 2.3.x + 1² = 9x² + 6x + 1
2) A área deste quadrado é m² + 8m + 16.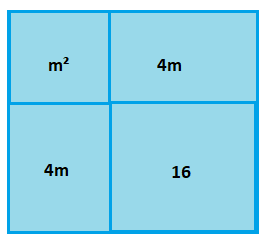
Observando a figura, diga quanto mede o lado desse quadrado.
RESPOSTA:
Vamos denominar as áreas das 4 figuras que formam o quadrado maior de A1, A2, A3 e A4.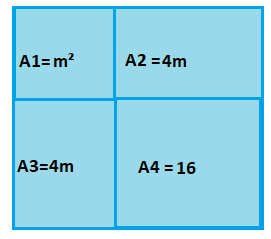
O quadrado de área A1 tem as medidas dos lados m, pois se sua área é m², a medida do seu lado será a raiz quadrada de m.
O quadrado de área A4 tem área igual a 16, portanto, a medida dos seus lados será a raiz quadrada de 16, que é 4.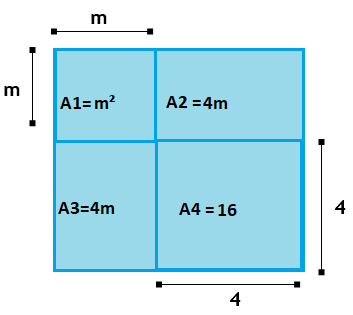
Se o quadrado de área A4 tem os lados iguais a 4, uma das medidas dos lados do retângulo A3 também será 4.
Se o quadrado de área A1 tem as medidas dos lados iguais a m, a outra medida do lado do retângulo de área A3 também será m.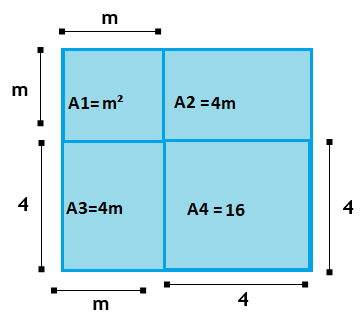
Agora, sabemos que o lado desse quadrado mede (m+4)
OUTRO MODO DE RESOLUÇÃO:
Portanto, o lado do quadrado tem medida igual a m+4.
