O triângulo equilátero é uma forma geométrica plana, que possui três lados com medidas iguais e com ângulos de 60°, totalizando uma área interna de 180°.
Para calcular as medidas do triângulo equilátero, usa-se o Teorema de Pitágoras, o qual estabelece fórmulas para encontrar a área, o perímetro e a altura de uma forma geométrica, com medidas iguais, tal como acontece com esse tipo de triângulo.
Área do triângulo equilátero
A área de uma figura é, no caso, o tamanho de sua superfície. Sendo assim, usa-se as diretrizes do teorema de Pitágoras para calcular a área do triângulo equilátero:
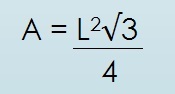
Sendo que:
- A= área;
- L= lado.
Perímetro
O perímetro de uma figura geométrica corresponde à soma de todos os lados da forma. Desse modo, é usada a seguinte fórmula, a fim de calcular o perímetro de um triângulo equilátero:
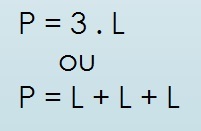
Sendo que:
- P = perímetro;
- L = lado.
Altura
A altura do triângulo equilátero mede-se por meio da multiplicação das medidas dos lados divididos por dois, ou seja:
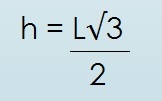
Sendo que:
- H = altura;
- L = lado.
Características do triângulo equilátero
Assim como toda forma geométrica, o triângulo equilátero possui algumas propriedades que dizem respeito somente a ele. São elas:
- Todo triângulo equilátero é isósceles
Os triângulos isósceles são aqueles que possuem dois lados iguais e um diferente. No caso, como todo triângulo equilátero tem os três lados iguais, também encaixa-se na determinação dos isósceles, podendo ser classificado nas duas formas matemáticas simultaneamente.
- Todos os ângulos do triângulo equilátero são congruentes
Como todos os lados do triângulo equilátero possuem medidas iguais, seus ângulos também são os mesmos: de 60°. Sabendo disso, ignora-se a necessidade de calcular tais medidas em eventuais exercícios matemáticos.
- Os ângulos externos de um triângulo equilátero medem 120°
Todos os ângulos do triângulo equilátero possuem 60°, totalizando 180° de área interna. Dessa forma, sabe-se que os ângulos externos dessa figura geométrica medem 120°.
- A bissetriz do triângulo retângulo é a mesma medida da altura do lado oposto a esse ângulo
A bissetriz é a reta que divide o ângulo ao meio. Tal medida, no triângulo equilátero, sempre terá a mesma grandeza do que a altura do lado oposto a esse ângulo. Essa conclusão é tirada por meio da semelhança entre os lados desse tipo de forma geométrica.
Isso quer dizer que, ao dividir um triângulo equilátero (mesmo que não seja ao meio), será formado dois triângulos diferentes, com medidas iguais.
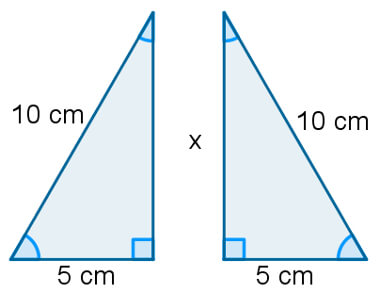
Exercícios resolvidos passo a passo
Para aprender a aplicar as fórmulas do triângulo equilátero, confira os exercícios resolvidos passo a passo, abaixo:
1) Numa maquete de um prédio, o arquiteto projetou um lago no formato de um triângulo. No entanto, para que o tipo específico de peixe sobreviva na água (o que foi uma exigência do cliente), é preciso saber qual é a área de plantas de oxigenação da água que será preciso completar. Sabendo que o triângulo tem medidas de 6cm na maquete, quanto de área precisará ser preenchida com as plantas?
- Primeiramente, aplica-se a fórmula da área:
A = L2√3/2 - Então, colocam-se as grandezas identificadas no enunciado:
A = 62√3/2 - Por fim, resolve-se a equação:
A = 36√3/2
A = 18√3cm2
2) Após uma maratona, um grupo de teatro organizou uma apresentação, que acontecerá dentro de um palco em formato de triângulo equilátero. No entanto, os organizadores precisam saber quanto é o perímetro da região, para certificarem onde deverão colocar os cones de isolamento da área. Sabendo que os lados a serem usados são de 60m, qual é o perímetro?
- Primeiramente, usa-se a fórmula do perímetro do triângulo equilátero:
P = 3 . L - Em seguida, transformam-se as medidas de 60m para centímetros, o que corresponde a 600cm:
- Então, colocam-se as grandezas na fórmula;
P = 3 . 600 - Resolve-se a equação;
P – 1800cm
Resultado é de 1800cm, ou 18m de perímetro.
3) Calcule a altura de um triângulo equilátero com lados que medem 4cm.
- Primeiramente, traça-se a altura do triângulo, dividindo a medida dos lados;
- Em seguida, aplica-se o teorema de Pitágoras, com as medidas destacadas:
a² + b² = c²
Por fim, resolve-se a equação:
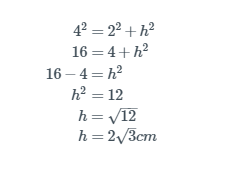Resultado da altura é de, aproximadamente, 3,4cm.
Para estudar mais sobre geometria, confira, também, os conteúdos sobre triângulo retângulo e triângulo isósceles.
