As equações são expressões algébricas que possuem uma incógnita que pode ter seu valor encontrado depois de realizadas algumas operações. Enquanto isso, as funções relacionam duas grandezas variáveis, ou seja, transformam um valor x em seu correspondente f(x).
Uma função pode assumir vários valores diferentes, dependendo da sua lei de formação e do valor de uma das variáveis. Já a equação conta como resultado apenas uma resposta certa.
Podemos perceber visualmente a diferença entre função e equação pelo modo como escrevemos cada uma.
A função é dada pela lei de formação em que geralmente aparece f(x) ou y igual a essa lei. Por exemplo:
- f(x) = 3x + 5
- y = x² + 3x + 1
Enquanto isso, a equação é escrita tendo apenas operações, uma incógnita e o sinal de igualdade. Por exemplo:
- 3n + 5 = 40
- 4x² + 5 – 35 = 15
- 2t = 0
O que são equações?
Equações são igualdades, ou seja, nelas aparece o sinal =. Além disso, elas apresentam um número desconhecido, chamado de incógnita. Fazendo a resolução correta, o valor encontrado é a solução da equação.
Portanto, ao contrário de funções que podem assumir diferentes valores, a equação possui apenas uma incógnita que tem valor único ou valores únicos, ou seja, existe apenas uma solução para uma determinada equação.
Geralmente, relacionamos equações com uma balança de dois pratos: nas balanças, você pode tirar ou adicionar nos dois pratos pesos iguais sem alterar o equilíbrio. Nas equações, o mesmo ocorre, você pode somar ou subtrair um mesmo valor dos dois lados, mantendo a igualdade. Você também pode multiplicar ou dividir os dois lados por um número, desde que ele não seja zero.
Fazemos isso em equações para isolarmos a incógnita.
Como resolver equações?
Considere a equação 3x + x/2 = 21. Fica mais fácil resolve-la se eliminarmos a fração x/2. Para isso, multiplique os dois lados por 2: 6x + x = 42.
Agora, basta isolarmos a incógnita:
- 7x = 42
- x = 42/7
- x = 6
Perceba que o valor da incógnita x pode apenas ser 6. Caso o seu resultado tenha dado outro valor, sua resolução está incorreta.
Em casos de equações com potências, a incógnita talvez possa assumir mais de um valor:
- x² – 1 = 0
- X = √1
- X = +1 ou x = –1.
O que são funções?
O matemático alemão Leibniz foi quem deu a denominação de função que usamos até hoje: expressões algébricas que indicam uma correspondência entre variáveis.
As funções relacionam duas grandezas variáveis. Por exemplo, aplicamos o conceito de função sempre que pagamos uma mercadoria, pois o valor a ser pago varia em função da quantidade de objetos comprados.
Por exemplo, se um caderno custa R$15,00, podemos chamar de x a quantidade de cadernos comprados e f(x) o preço final dessa compra. A função do valor a ser pago em relação à quantidade de cadernos comprados pode ser então dada por:
- f(x) = 15x
As funções são muito usadas na ciência, já que elas são praticamente uma “fórmula” ou um “modelo matemático” para descrever fenômenos e possibilitar previsões de resultados.
Noção de função por meio de conjuntos
Observe, abaixo, dois conjuntos denominados A e B. Todos os elementos de A, ao serem multiplicados por 3, resultam em um número que é encontrado no conjunto B.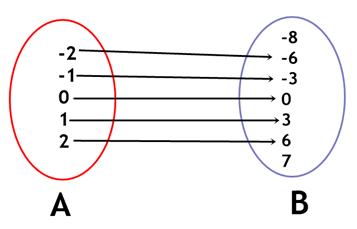 Todos os elementos de A têm correspondente em B e cada elemento de A possui um único elemento de B. Nesse caso, temos uma função de A em B, expressa pela fórmula y = 3x.
Todos os elementos de A têm correspondente em B e cada elemento de A possui um único elemento de B. Nesse caso, temos uma função de A em B, expressa pela fórmula y = 3x.
Portanto, podemos então definir função como: dados dois conjuntos A e B, uma função de A em B é uma regra que indica como associar cada elemento de x pertencente ao conjunto A a um único elemento y pertencente ao conjunto B.
Exercícios resolvidos
1) Diga se as seguintes expressões algébricas são equações ou funções.
a) f(x) = x² + 2x + 27
b) v(t) = vo + at
c) 3x + 5x = 3 + x/2
d) 4n + 2/n = n²
e) F = n + 1
RESPOSTA:
a) função
b) função
c) equação
d) equação
e) equação
As propriedades da potenciação são ferramentas que simplificam operações envolvendo exponenciação. Conheça cada uma delas!
👉 Continue Lendo.. Clique aqui





