Sistematizada na obra “Os Elementos”, do matemático grego Euclides de Alexandria (320-270 a.C.), a área matemática da Geometria de Posição estuda as posições relativas entre as formas geométricas localizadas espacialmente. Seu principal foco está no estudo dos três princípios fundamentais da geometria no espaço: ponto, reta e plano. Além disso, as principais noções são as de forma, tamanho e posição.
Já os poliedros são figuras geométricas espaciais que possuem vértices, arestas e faces, sendo estes sólidos limitados por polígonos, ou seja, figuras fechadas com lados formados por retas, como triângulos e quadrados.
Conceitos Primitivos e Postulados da Geometria de Posição
Os Conceitos Primitivos são as representações básicas, não tendo uma definição que os anteceda dentro da geometria, assim, estes são considerados como noções primitivas, sendo: ponto, reta, plano e espaço.
Todos os conceitos se relacionam entre si a partir de diversos postulados, ou seja, verdades incontestáveis. O postulado fundamental desses primitivos é a existência de uma infinidade de pontos, retas e planos no espaço.
O ponto tem a característica de não possuir dimensão e sempre ser indicado por letras maiúsculas, além disso, possui o postulado de ter infinitas retas passando por ele.
A reta, por sua vez, é unidimensional e é representada por letras minúsculas. Esta ainda apresenta o postulado de que dentro de uma reta há a presença de infinitos pontos, e o postulado de que dois pontos determinam um segmento de uma reta. Além disso, um ponto divide a reta em duas partes e cada parte será uma semirreta.
A reta também pode possuir as seguintes classificações:
- Retas concorrentes: possuem apenas um ponto comum;
- Retas paralelas: não têm um ponto comum;
- Retas reversas: não possuem um plano que as contenha e nem o admitem ponto comum;
- Retas perpendiculares: duas retas concorrentes que formam ângulo reto;
- Retas ortogonais: são retas reversas que formam um ângulo reto;
- Retas coincidentes: possuem todos os seus pontos em comum, estão sobrepostas.
 Por sua vez, o plano tem a característica de ser bidimensional, apresentando largura e comprimento, e sendo indicado por letras do alfabeto grego, como alfa (α). Este possui o postulado de conter infinitos pontos e infinitas retas e o postulado de que três pontos distintos e não colineares determinam um único plano.
Por sua vez, o plano tem a característica de ser bidimensional, apresentando largura e comprimento, e sendo indicado por letras do alfabeto grego, como alfa (α). Este possui o postulado de conter infinitos pontos e infinitas retas e o postulado de que três pontos distintos e não colineares determinam um único plano.
Além disso, uma reta pode dividir um plano em dois semiplanos, sendo essa a que origina dois desses opostamente. O plano também divide o espaço em dois semiespaços, além de poder ser determinado das seguintes formas: por uma reta e um ponto fora desta; por duas retas concorrentes; e por duas retas paralelas distintas.
O espaço tem a característica de ser tridimensional e de ser o conjunto com infinitos pontos, infinitas retas e infinitos planos.
Exercício- (UEL) Sobre os conhecimentos de geometria tridimensional, considere as afirmativas:
I. Se duas retas distintas não são paralelas, então elas são concorrentes.
II. Três pontos distintos entre si determinam um único plano.
III. Duas retas paralelas distintas determinam um plano.
IV. Se duas retas r e s são reversas, então existe um único plano á que contém r e é paralelo a s.
A alternativa que contém todas as afirmativas corretas é:
a) I e II.
b) I e IV.
c)III e IV.
d)I, II e III.
e) II, III e IV.
Resolução:
I. Incorreta, pois retas concorrentes possuem um ponto comum, diferente das retas paralelas.
II. Correta, pois, segundo um dos postulados do plano, três pontos distintos e não colineares determinam um único plano.
III. Correta, pois um plano pode ser determinado por duas retas paralelas distintas.
IV. Incorreta, pois retas reversas não possuem um plano que as contenha e nem o admitem ponto comum.
Dessa forma, a alternativa correta é a C.
Poliedros: o que são e seus elementos
Os poliedros são formados por faces, arestas e vértices, possuindo três dimensões. As faces de um poliedro são formadas por planos, sendo cada uma dessas um polígono (figura fechada com lados formados por retas). Duas faces de um poliedro nunca estão no mesmo plano, mas estão no mesmo espaço. Já as arestas são os segmentos de reta provenientes do encontro entre duas faces distintas. Por fim, os vértices são os pontos de encontro das arestas.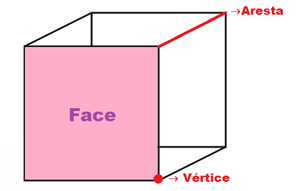
Tipos de poliedros
- Poliedros regulares: esses poliedros foram estudados pelo filósofo grego Platão e possuem faces compostas por polígonos iguais e regulares, além de serem convexos. Exemplo: cubo e tetraedro;
- Prismas: duas bases congruentes e paralelas, tendo faces laterais que são paralelogramos;
- Pirâmide: apresenta um polígono como base e um vértice que une todas as faces laterais triangulares;
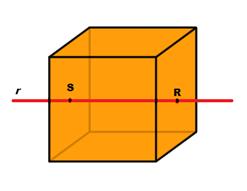
- Poliedro convexo: poliedro que contém segmento com extremidades em seu interior totalmente contidas no poliedro.
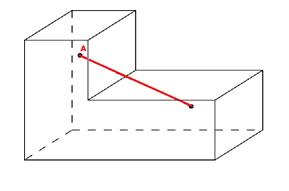
- Poliedro côncavo: contém segmento com extremidades dentro do poliedro com pontos fora do poliedro.
Teorema de Euler
Com a seguinte fórmula, formulada pelo matemático suíço Leonhard Euler, é possível verificar, comprovar e relacionar o número de faces, arestas e vértices de poliedros convexos:
- V + F = 2 + A – Sendo: V= vértices; F= faces; A= arestas.
Por exemplo, um cubo tem 8 vértices, 6 faces e 12 arestas, colocando na fórmula: 8+6=2+12.
Exercícios – (FAAP-SP) Num poliedro convexo, o número de arestas excede o número de vértices em 6 unidades. Calcule o número de faces.
Resolução:
Utilizando o Teorema de Euler (V + F = 2 + A), o número de arestas excede os vértices em 6 unidades, então: A= V+6.
Substituindo na fórmula:
V + F = 2 + V +6.
Passando o V para o outro lado (muda-se o sinal):
V+F-V=2+6
F=8
Assim, o número de faces é 8.
As propriedades da potenciação são ferramentas que simplificam operações envolvendo exponenciação. Conheça cada uma delas!
👉 Continue Lendo.. Clique aqui





