Quando estamos lidando com figuras planas, dois conceitos que devemos saber são área e perímetro.
A área de um local nos diz a quantidade de espaço bidimensional dessa região. Ela é dada a partir de uma unidade de medida, que pode ser em cm², m², etc. Portanto, ela nos informa quantos quadrados de 1cm de lado ou 1m de lado conseguimos colocar dentro de uma região, por exemplo.
Enquanto isso, o perímetro irá medir o contorno do local. Essa medida é dada também a partir de uma unidade, que pode ser metros, centímetros…
[VEJA TAMBÉM: FORMAS GEOMÉTRICAS – CÍRCULO, TRIÂNGULO, HEXÁGONO…]
Quando utilizamos área e perímetro?
Quando estamos reformando uma casa, por exemplo, para comprarmos uma quantidade certa de rodapés, devemos medir o perímetro do cômodo, ou seja, somar a medida de cada lado e descontar a medida das portas.
Quando vamos comprar um terreno, uma maneira de imaginar qual o seu tamanho, sem ter que o visitar, é se informar sobre a sua área.
Perímetro de um contorno
Como já foi dito, podemos definir perímetro como o comprimento de um contorno. No caso de polígonos, o perímetro é basicamente a soma das medidas dos comprimentos dos lados.
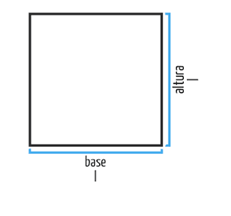
Em um quadrado, seus quatro lados possuem a mesma medida. Chamando essa medida de L, podemos calcular o seu perímetro da seguinte maneira:
Perímetro = L + L + L + L = 4.L
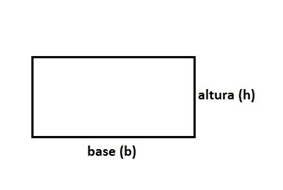
Em um retângulo, temos dois pares de lados iguais. Sendo B a medida de um dos lados e H a medida do outro lado, teremos o perímetro do retângulo dado por:
Perímetro = B + B + H + H = 2B + 2H
Em um triângulo equilátero, os seus 3 lados possuem a mesma medida. Sendo L a medida de um desses lados, podemos então calcular seu perímetro fazendo:
Perímetro = L + L + L = 3.L
Em um triângulo Isósceles, dois de seus lados possuem a mesma medida. Chamando de X a medida do par de lados iguais e Y a medida do terceiro lado, podemos definir o perímetro como:
Perímetro = 2X + Y
Comprimento de uma circunferência
No caso de um círculo, a medida do diâmetro é chamada de comprimento da circunferência, e é dada por:
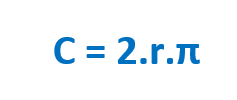
Sendo C o comprimento, r a medida do raio e π uma constante de valor aproximado igual a 3,14.
Área de uma superfície
Vamos pensar no seguinte exemplo: Larissa quer cobrir a mesa com folhas de papel. Para isso, ela utilizou, ao todo, 10 folhas iguais. Isso significa que o tampo da mesa tem área de 10 unidades, considerando uma folha como unidade.
Geralmente, utilizamos como a nossa unidade de medida metros e centímetros. Quando dizemos que um terreno tem 18 m², estamos dizendo que dentro dele existem 18 quadrados de 1m de lado.
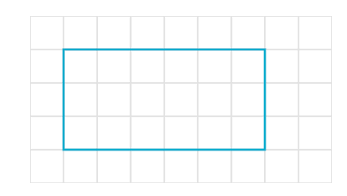
Observe: o retângulo abaixo está numa malha quadriculada com quadrados de 1cm de lado. Ele possui uma altura de 3 quadrados e uma base de 6 quadrados. Para calcularmos sua área, basta fazer 3×6 = 18 cm². Veja que há exatamente 18 quadrados dentro dele.
Área de regiões
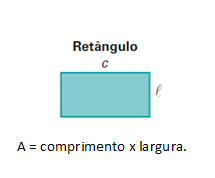
Área do retângulo: para calcularmos sua área, basta multiplicar a medida do comprimento pela largura.
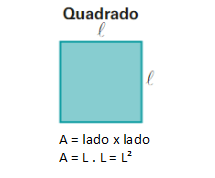
Área do Quadrado: nesse caso, vamos fazer o mesmo que fizemos acima. Lembrando que o quadrado tem os 4 lados de mesma medida, faremos:
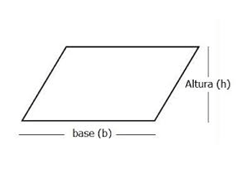
Área do Paralelogramo: A = Base x altura = b.h
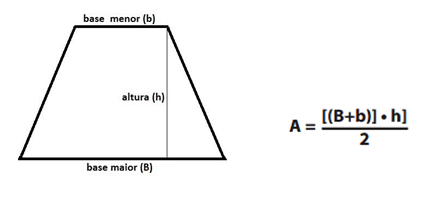
Área do Trapézio: sendo b a medida da base menor, h a medida da altura e B a medida da base maior, calcularemos a área da seguinte maneira:
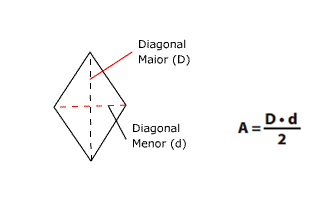
Área do losango: sendo D a medida da diagonal maior e d a medida da diagonal menor, faremos:
Área de triângulos
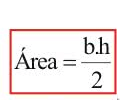
Triângulo retângulo: se soubermos a medida da altura e da base, podemos calcular por A = b.h/2 sendo b a medida da base e h a medida da altura.
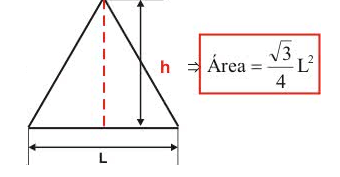
Triângulo equilátero: podemos calcular sua área sabendo a medida de um dos seus lados. Utilizamos, então, a fórmula abaixo:
Outros triângulos: utilizaremos a mesma formula do triângulo retângulo.
Exercícios Resolvidos
1) Um terreno quadrado tem 400m² de área. Quanto mede o lado desse terreno?
_______________________
_______________________
_______________________
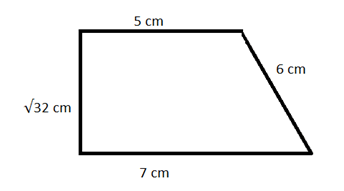
2) Calcule o perímetro da figura abaixo:
RESPOSTAS:
1.
A = l²
400 = l²
√400 = l
l = 20 metros
2. √32 + 5 + 6 + 7 = 18 + √32 cm
